Relative Entailment Among Probabilistic Implications

We study a natural variant of the implicational fragment of propositional logic. Its formulas are pairs of conjunctions of positive literals, related together by an implicational-like connective; the semantics of this sort of implication is defined in terms of a threshold on a conditional probability of the consequent, given the antecedent: we are dealing with what the data analysis community calls confidence of partial implications or association rules. Existing studies of redundancy among these partial implications have characterized so far only entailment from one premise and entailment from two premises, both in the stand-alone case and in the case of presence of additional classical implications (this is what we call "relative entailment"). By exploiting a previously noted alternative view of the entailment in terms of linear programming duality, we characterize exactly the cases of entailment from arbitrary numbers of premises, again both in the stand-alone case and in the case of presence of additional classical implications. As a result, we obtain decision algorithms of better complexity; additionally, for each potential case of entailment, we identify a critical confidence threshold and show that it is, actually, intrinsic to each set of premises and antecedent of the conclusion.

Clause-Learning Algorithms with Many Restarts and Bounded-Width Resolution

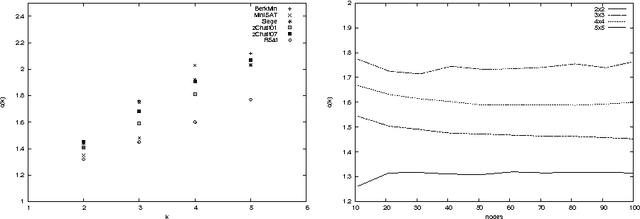
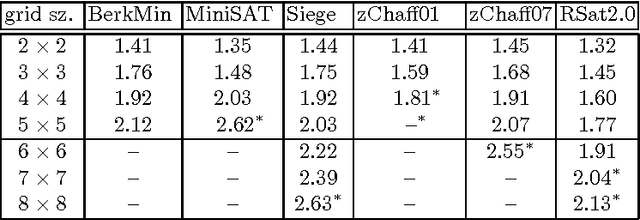
We offer a new understanding of some aspects of practical SAT-solvers that are based on DPLL with unit-clause propagation, clause-learning, and restarts. We do so by analyzing a concrete algorithm which we claim is faithful to what practical solvers do. In particular, before making any new decision or restart, the solver repeatedly applies the unit-resolution rule until saturation, and leaves no component to the mercy of non-determinism except for some internal randomness. We prove the perhaps surprising fact that, although the solver is not explicitly designed for it, with high probability it ends up behaving as width-k resolution after no more than O(n^2k+2) conflicts and restarts, where n is the number of variables. In other words, width-k resolution can be thought of as O(n^2k+2) restarts of the unit-resolution rule with learning.