TE-ETH: Lower Bounds for QBFs of Bounded Treewidth

The problem of deciding the validity (QSAT) of quantified Boolean formulas (QBF) is a vivid research area in both theory and practice. In the field of parameterized algorithmics, the well-studied graph measure treewidth turned out to be a successful parameter. A well-known result by Chen in parameterized complexity is that QSAT when parameterized by the treewidth of the primal graph of the input formula together with the quantifier depth of the formula is fixed-parameter tractable. More precisely, the runtime of such an algorithm is polynomial in the formula size and exponential in the treewidth, where the exponential function in the treewidth is a tower, whose height is the quantifier depth. A natural question is whether one can significantly improve these results and decrease the tower while assuming the Exponential Time Hypothesis (ETH). In the last years, there has been a growing interest in the quest of establishing lower bounds under ETH, showing mostly problem-specific lower bounds up to the third level of the polynomial hierarchy. Still, an important question is to settle this as general as possible and to cover the whole polynomial hierarchy. In this work, we show lower bounds based on the ETH for arbitrary QBFs parameterized by treewidth (and quantifier depth). More formally, we establish lower bounds for QSAT and treewidth, namely, that under ETH there cannot be an algorithm that solves QSAT of quantifier depth i in runtime significantly better than i-fold exponential in the treewidth and polynomial in the input size. In doing so, we provide a versatile reduction technique to compress treewidth that encodes the essence of dynamic programming on arbitrary tree decompositions. Further, we describe a general methodology for a more fine-grained analysis of problems parameterized by treewidth that are at higher levels of the polynomial hierarchy.

Backdoors to Tractable Answer-Set Programming

Answer Set Programming (ASP) is an increasingly popular framework for declarative programming that admits the description of problems by means of rules and constraints that form a disjunctive logic program. In particular, many AI problems such as reasoning in a nonmonotonic setting can be directly formulated in ASP. Although the main problems of ASP are of high computational complexity, located at the second level of the Polynomial Hierarchy, several restrictions of ASP have been identified in the literature, under which ASP problems become tractable. In this paper we use the concept of backdoors to identify new restrictions that make ASP problems tractable. Small backdoors are sets of atoms that represent "clever reasoning shortcuts" through the search space and represent a hidden structure in the problem input. The concept of backdoors is widely used in the areas of propositional satisfiability and constraint satisfaction. We show that it can be fruitfully adapted to ASP. We demonstrate how backdoors can serve as a unifying framework that accommodates several tractable restrictions of ASP known from the literature. Furthermore, we show how backdoors allow us to deploy recent algorithmic results from parameterized complexity theory to the domain of answer set programming.

Clause-Learning Algorithms with Many Restarts and Bounded-Width Resolution

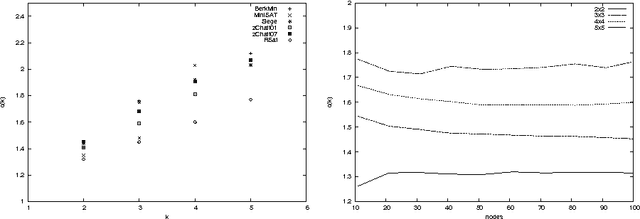
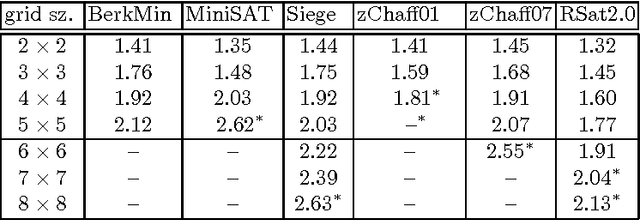
We offer a new understanding of some aspects of practical SAT-solvers that are based on DPLL with unit-clause propagation, clause-learning, and restarts. We do so by analyzing a concrete algorithm which we claim is faithful to what practical solvers do. In particular, before making any new decision or restart, the solver repeatedly applies the unit-resolution rule until saturation, and leaves no component to the mercy of non-determinism except for some internal randomness. We prove the perhaps surprising fact that, although the solver is not explicitly designed for it, with high probability it ends up behaving as width-k resolution after no more than O(n^2k+2) conflicts and restarts, where n is the number of variables. In other words, width-k resolution can be thought of as O(n^2k+2) restarts of the unit-resolution rule with learning.

Backdoors to Normality for Disjunctive Logic Programs

Over the last two decades, propositional satisfiability (SAT) has become one of the most successful and widely applied techniques for the solution of NP-complete problems. The aim of this paper is to investigate theoretically how Sat can be utilized for the efficient solution of problems that are harder than NP or co-NP. In particular, we consider the fundamental reasoning problems in propositional disjunctive answer set programming (ASP), Brave Reasoning and Skeptical Reasoning, which ask whether a given atom is contained in at least one or in all answer sets, respectively. Both problems are located at the second level of the Polynomial Hierarchy and thus assumed to be harder than NP or co-NP. One cannot transform these two reasoning problems into SAT in polynomial time, unless the Polynomial Hierarchy collapses. We show that certain structural aspects of disjunctive logic programs can be utilized to break through this complexity barrier, using new techniques from Parameterized Complexity. In particular, we exhibit transformations from Brave and Skeptical Reasoning to SAT that run in time O(2^k n^2) where k is a structural parameter of the instance and n the input size. In other words, the reduction is fixed-parameter tractable for parameter k. As the parameter k we take the size of a smallest backdoor with respect to the class of normal (i.e., disjunction-free) programs. Such a backdoor is a set of atoms that when deleted makes the program normal. In consequence, the combinatorial explosion, which is expected when transforming a problem from the second level of the Polynomial Hierarchy to the first level, can now be confined to the parameter k, while the running time of the reduction is polynomial in the input size n, where the order of the polynomial is independent of k.

The Good, the Bad, and the Odd: Cycles in Answer-Set Programs

Backdoors of answer-set programs are sets of atoms that represent clever reasoning shortcuts through the search space. Assignments to backdoor atoms reduce the given program to several programs that belong to a tractable target class. Previous research has considered target classes based on notions of acyclicity where various types of cycles (good and bad cycles) are excluded from graph representations of programs. We generalize the target classes by taking the parity of the number of negative edges on bad cycles into account and consider backdoors for such classes. We establish new hardness results and non-uniform polynomial-time tractability relative to directed or undirected cycles.