Clause-Learning Algorithms with Many Restarts and Bounded-Width Resolution

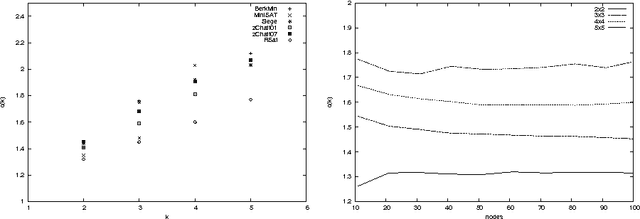
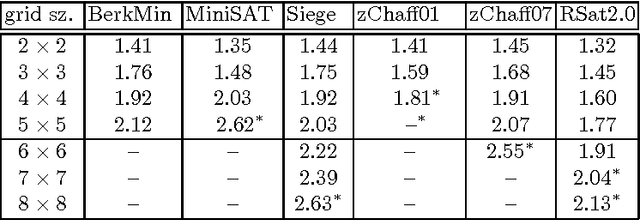
We offer a new understanding of some aspects of practical SAT-solvers that are based on DPLL with unit-clause propagation, clause-learning, and restarts. We do so by analyzing a concrete algorithm which we claim is faithful to what practical solvers do. In particular, before making any new decision or restart, the solver repeatedly applies the unit-resolution rule until saturation, and leaves no component to the mercy of non-determinism except for some internal randomness. We prove the perhaps surprising fact that, although the solver is not explicitly designed for it, with high probability it ends up behaving as width-k resolution after no more than O(n^2k+2) conflicts and restarts, where n is the number of variables. In other words, width-k resolution can be thought of as O(n^2k+2) restarts of the unit-resolution rule with learning.