On the class of coding optimality of human languages and the origins of Zipf's law

Here we present a new class of optimality for coding systems. Members of that class are separated linearly from optimal coding and thus exhibit Zipf's law, namely a power-law distribution of frequency ranks. Whithin that class, Zipf's law, the size-rank law and the size-probability law form a group-like structure. We identify human languages that are members of the class. All languages showing sufficient agreement with Zipf's law are potential members of the class. In contrast, there are communication systems in other species that cannot be members of that class for exhibiting an exponential distribution instead but dolphins and humpback whales might. We provide a new insight into plots of frequency versus rank in double logarithmic scale. For any system, a straight line in that scale indicates that the lengths of optimal codes under non-singular coding and under uniquely decodable encoding are separated by a linear function whose slope is the exponent of Zipf's law. For systems under compression and constrained to be uniquely decodable, such a straight line may indicate that the system is coding close to optimality. Our findings provide support for the hypothesis that Zipf's law originates from compression.

The exponential distribution of the orders of demonstrative, numeral, adjective and noun

The frequency of the preferred order for a noun phrase formed by demonstrative, numeral, adjective and noun has received significant attention over the last two decades. We investigate the actual distribution of the preferred 24 possible orders. There is no consensus on whether it can be well-fitted by an exponential or a power law distribution. We find that an exponential distribution is a much better model. This finding and other circumstances where an exponential-like distribution is found challenge the view that power-law distributions, e.g., Zipf's law for word frequencies, are inevitable. We also investigate which of two exponential distributions gives a better fit: an exponential model where the 24 orders have non-zero probability or an exponential model where the number of orders that can have non-zero probability is variable. When parsimony and generalizability are prioritized, we find strong support for the exponential model where all 24 orders have non-zero probability. This finding suggests that there is no hard constraint on word order variation and then unattested orders merely result from undersampling, consistently with Cysouw's view.

Who is the root in a syntactic dependency structure?

The syntactic structure of a sentence can be described as a tree that indicates the syntactic relationships between words. In spite of significant progress in unsupervised methods that retrieve the syntactic structure of sentences, guessing the right direction of edges is still a challenge. As in a syntactic dependency structure edges are oriented away from the root, the challenge of guessing the right direction can be reduced to finding an undirected tree and the root. The limited performance of current unsupervised methods demonstrates the lack of a proper understanding of what a root vertex is from first principles. We consider an ensemble of centrality scores, some that only take into account the free tree (non-spatial scores) and others that take into account the position of vertices (spatial scores). We test the hypothesis that the root vertex is an important or central vertex of the syntactic dependency structure. We confirm that hypothesis and find that the best performance in guessing the root is achieved by novel scores that only take into account the position of a vertex and that of its neighbours. We provide theoretical and empirical foundations towards a universal notion of rootness from a network science perspective.

Predictability maximization and the origins of word order harmony

We address the linguistic problem of the sequential arrangement of a head and its dependents from an information theoretic perspective. In particular, we consider the optimal placement of a head that maximizes the predictability of the sequence. We assume that dependents are statistically independent given a head, in line with the open-choice principle and the core assumptions of dependency grammar. We demonstrate the optimality of harmonic order, i.e., placing the head last maximizes the predictability of the head whereas placing the head first maximizes the predictability of dependents. We also show that postponing the head is the optimal strategy to maximize its predictability while bringing it forward is the optimal strategy to maximize the predictability of dependents. We unravel the advantages of the strategy of maximizing the predictability of the head over maximizing the predictability of dependents. Our findings shed light on the placements of the head adopted by real languages or emerging in different kinds of experiments.

Swap distance minimization beyond entropy minimization in word order variation

Here we consider the problem of all the possible orders of a linguistic structure formed by $n$ elements, for instance, subject, direct object and verb ($n=3$) or subject, direct object, indirect object and verb ($n=4$). We investigate if the frequency of the $n!$ possible orders is constrained by two principles. First, entropy minimization, a principle that has been suggested to shape natural communication systems at distinct levels of organization. Second, swap distance minimization, namely a preference for word orders that require fewer swaps of adjacent elements to be produced from a source order. Here we present average swap distance, a novel score for research on swap distance minimization, and investigate the theoretical distribution of that score for any $n$: its minimum and maximum values and its expected value in die rolling experiments or when the word order frequencies are shuffled. We investigate whether entropy and average swap distance are significantly small in distinct linguistic structures with $n=3$ or $n=4$ in agreement with the corresponding minimization principles. We find strong evidence of entropy minimization and swap distance minimization with respect to a die rolling experiment. The evidence of these two forces with respect to a Polya urn process is strong for $n=4$ but weaker for $n=3$. We still find evidence of swap distance minimization when word order frequencies are shuffled, indicating that swap distance minimization effects are beyond pressure to minimize word order entropy.

The optimal placement of the head in the noun phrase. The case of demonstrative, numeral, adjective and noun

The word order of a sentence is shaped by multiple principles. The principle of syntactic dependency distance minimization is in conflict with the principle of surprisal minimization (or predictability maximization) in single head syntactic dependency structures: while the former predicts that the head should be placed at the center of the linear arrangement, the latter predicts that the head should be placed at one of the ends (either first or last). A critical question is when surprisal minimization (or predictability maximization) should surpass syntactic dependency distance minimization. In the context of single head structures, it has been predicted that this is more likely to happen when two conditions are met, i.e. (a) fewer words are involved and (b) words are shorter. Here we test the prediction on the noun phrase when it is composed of a demonstrative, a numeral, an adjective and a noun. We find that, across preferred orders in languages, the noun tends to be placed at one of the ends, confirming the theoretical prediction. We also show evidence of anti locality effects: syntactic dependency distances in preferred orders are longer than expected by chance.

Swap distance minimization in SOV languages. Cognitive and mathematical foundations

Distance minimization is a general principle of language. A special case of this principle in the domain of word order is swap distance minimization. This principle predicts that variations from a canonical order that are reached by fewer swaps of adjacent constituents are lest costly and thus more likely. Here we investigate the principle in the context of the triple formed by subject (S), object (O) and verb (V). We introduce the concept of word order rotation as a cognitive underpinning of that prediction. When the canonical order of a language is SOV, the principle predicts SOV < SVO, OSV < VSO, OVS < VOS, in order of increasing cognitive cost. We test the prediction in three flexible order SOV languages: Korean (Koreanic), Malayalam (Dravidian), and Sinhalese (Indo-European). Evidence of swap distance minimization is found in all three languages, but it is weaker in Sinhalese. Swap distance minimization is stronger than a preference for the canonical order in Korean and especially Malayalam.

Linguistic laws in biology

Linguistic laws, the common statistical patterns of human language, have been investigated by quantitative linguists for nearly a century. Recently, biologists from a range of disciplines have started to explore the prevalence of these laws beyond language, finding patterns consistent with linguistic laws across multiple levels of biological organisation, from molecular (genomes, genes, and proteins) to organismal (animal behaviour) to ecological (populations and ecosystems). We propose a new conceptual framework for the study of linguistic laws in biology, comprising and integrating distinct levels of analysis, from description to prediction to theory building. Adopting this framework will provide critical new insights into the fundamental rules of organisation underpinning natural systems, unifying linguistic laws and core theory in biology.

Direct and indirect evidence of compression of word lengths. Zipf's law of abbreviation revisited

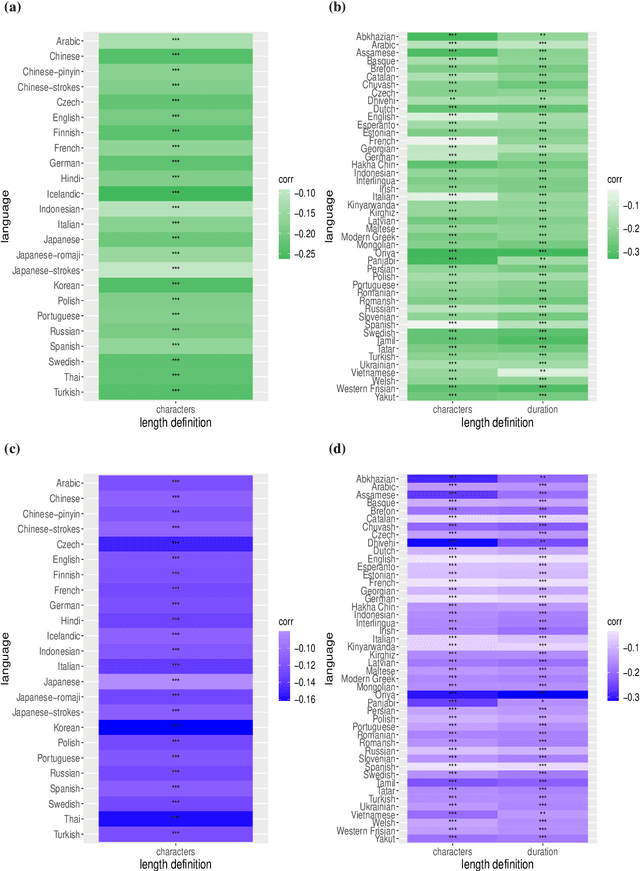
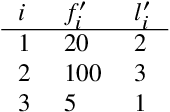
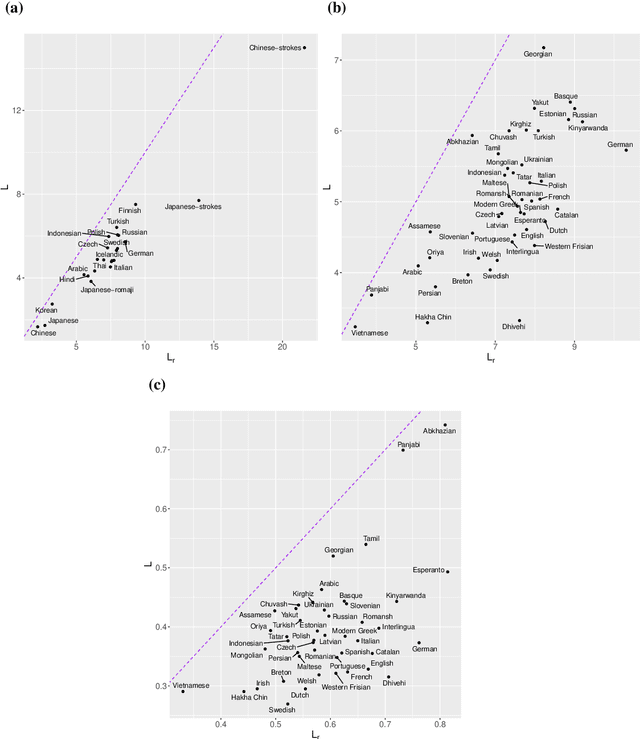
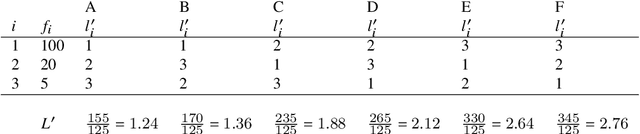
Zipf's law of abbreviation, the tendency of more frequent words to be shorter, is one of the most solid candidates for a linguistic universal, in the sense that it has the potential for being exceptionless or with a number of exceptions that is vanishingly small compared to the number of languages on Earth. Since Zipf's pioneering research, this law has been viewed as a manifestation of a universal principle of communication, i.e. the minimization of word lengths, to reduce the effort of communication. Here we revisit the concordance of written language with the law of abbreviation. Crucially, we provide wider evidence that the law holds also in speech (when word length is measured in time), in particular in 46 languages from 14 linguistic families. Agreement with the law of abbreviation provides indirect evidence of compression of languages via the theoretical argument that the law of abbreviation is a prediction of optimal coding. Motivated by the need of direct evidence of compression, we derive a simple formula for a random baseline indicating that word lengths are systematically below chance, across linguistic families and writing systems, and independently of the unit of measurement (length in characters or duration in time). Our work paves the way to measure and compare the degree of optimality of word lengths in languages.

The distribution of syntactic dependency distances

The syntactic structure of a sentence can be represented as a graph where vertices are words and edges indicate syntactic dependencies between them. In this setting, the distance between two syntactically linked words can be defined as the difference between their positions. Here we want to contribute to the characterization of the actual distribution of syntactic dependency distances, and unveil its relationship with short-term memory limitations. We propose a new double-exponential model in which decay in probability is allowed to change after a break-point. This transition could mirror the transition from the processing of words chunks to higher-level structures. We find that a two-regime model -- where the first regime follows either an exponential or a power-law decay -- is the most likely one in all 20 languages we considered, independently of sentence length and annotation style. Moreover, the break-point is fairly stable across languages and averages values of 4-5 words, suggesting that the amount of words that can be simultaneously processed abstracts from the specific language to a high degree. Finally, we give an account of the relation between the best estimated model and the closeness of syntactic dependencies, as measured by a recently introduced optimality score.