Direct and indirect evidence of compression of word lengths. Zipf's law of abbreviation revisited

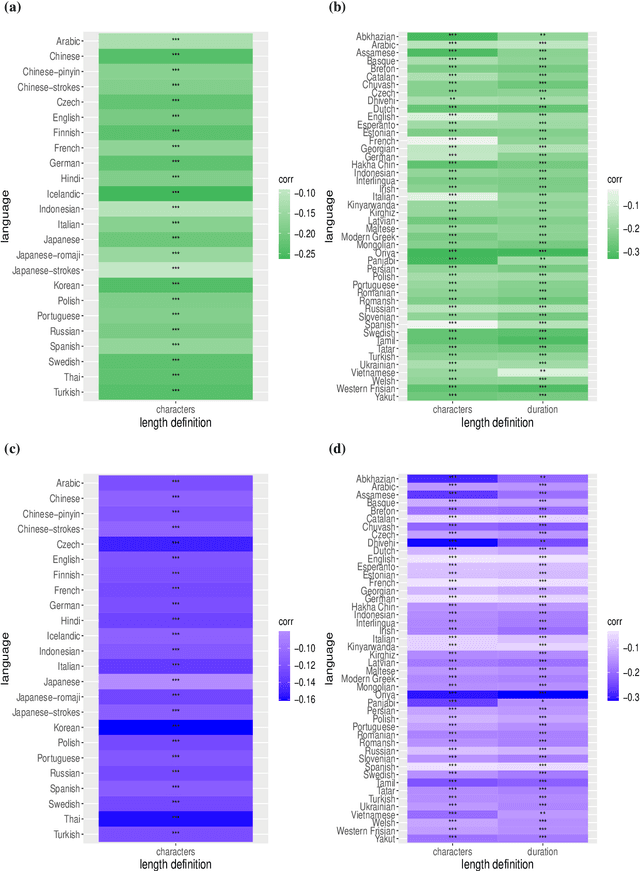
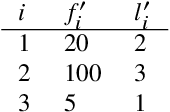
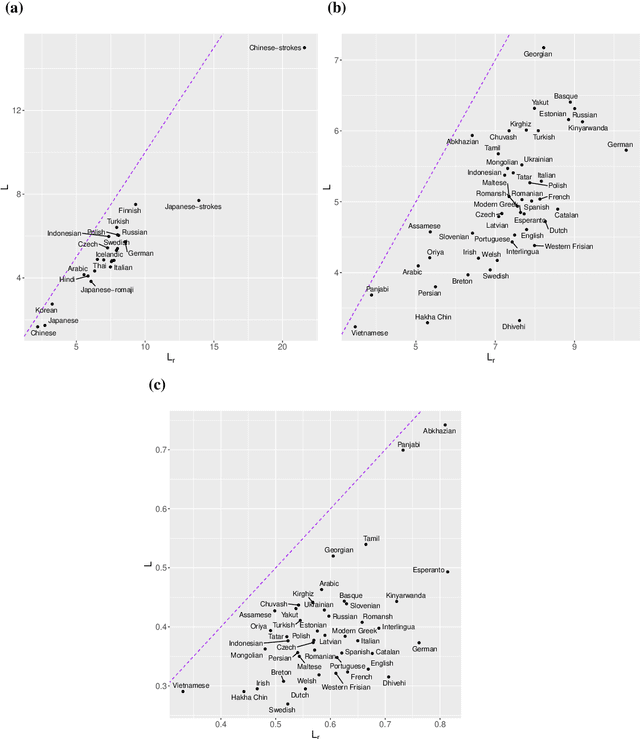
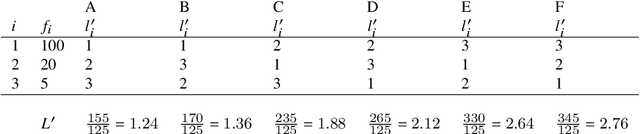
Zipf's law of abbreviation, the tendency of more frequent words to be shorter, is one of the most solid candidates for a linguistic universal, in the sense that it has the potential for being exceptionless or with a number of exceptions that is vanishingly small compared to the number of languages on Earth. Since Zipf's pioneering research, this law has been viewed as a manifestation of a universal principle of communication, i.e. the minimization of word lengths, to reduce the effort of communication. Here we revisit the concordance of written language with the law of abbreviation. Crucially, we provide wider evidence that the law holds also in speech (when word length is measured in time), in particular in 46 languages from 14 linguistic families. Agreement with the law of abbreviation provides indirect evidence of compression of languages via the theoretical argument that the law of abbreviation is a prediction of optimal coding. Motivated by the need of direct evidence of compression, we derive a simple formula for a random baseline indicating that word lengths are systematically below chance, across linguistic families and writing systems, and independently of the unit of measurement (length in characters or duration in time). Our work paves the way to measure and compare the degree of optimality of word lengths in languages.