Towards a Law of Iterated Expectations for Heuristic Estimators

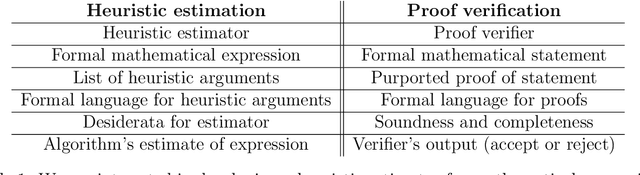
Christiano et al. (2022) define a *heuristic estimator* to be a hypothetical algorithm that estimates the values of mathematical expressions from arguments. In brief, a heuristic estimator $\mathbb{G}$ takes as input a mathematical expression $Y$ and a formal "heuristic argument" $\pi$, and outputs an estimate $\mathbb{G}(Y \mid \pi)$ of $Y$. In this work, we argue for the informal principle that a heuristic estimator ought not to be able to predict its own errors, and we explore approaches to formalizing this principle. Most simply, the principle suggests that $\mathbb{G}(Y - \mathbb{G}(Y \mid \pi) \mid \pi)$ ought to equal zero for all $Y$ and $\pi$. We argue that an ideal heuristic estimator ought to satisfy two stronger properties in this vein, which we term *iterated estimation* (by analogy to the law of iterated expectations) and *error orthogonality*. Although iterated estimation and error orthogonality are intuitively appealing, it can be difficult to determine whether a given heuristic estimator satisfies the properties. As an alternative approach, we explore *accuracy*: a property that (roughly) states that $\mathbb{G}$ has zero average error over a distribution of mathematical expressions. However, in the context of two estimation problems, we demonstrate barriers to creating an accurate heuristic estimator. We finish by discussing challenges and potential paths forward for finding a heuristic estimator that accords with our intuitive understanding of how such an estimator ought to behave, as well as the potential applications of heuristic estimators to understanding the behavior of neural networks.

Backdoor defense, learnability and obfuscation

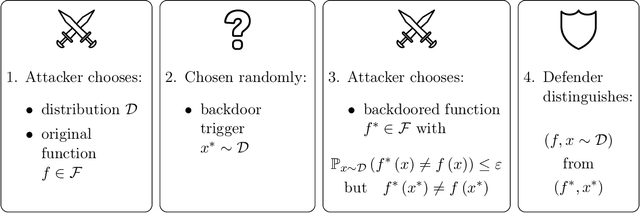
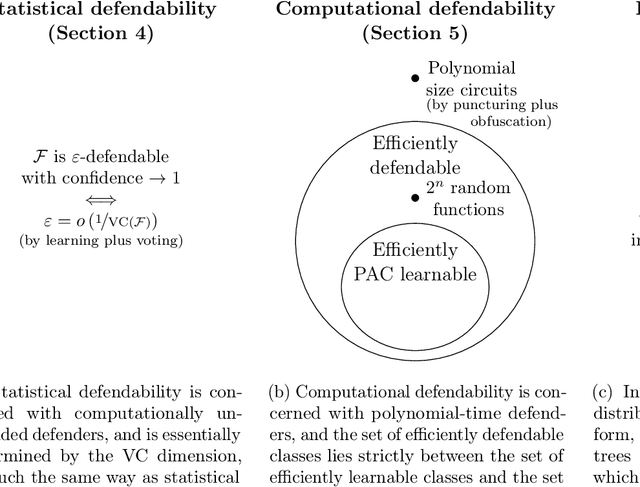
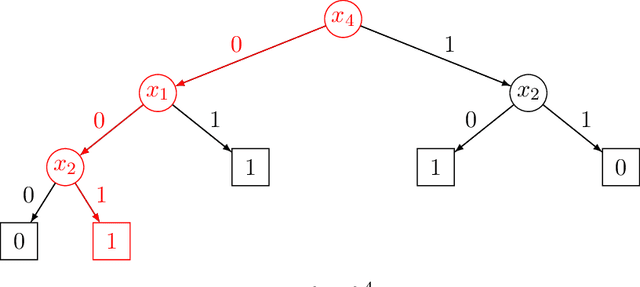
We introduce a formal notion of defendability against backdoors using a game between an attacker and a defender. In this game, the attacker modifies a function to behave differently on a particular input known as the "trigger", while behaving the same almost everywhere else. The defender then attempts to detect the trigger at evaluation time. If the defender succeeds with high enough probability, then the function class is said to be defendable. The key constraint on the attacker that makes defense possible is that the attacker's strategy must work for a randomly-chosen trigger. Our definition is simple and does not explicitly mention learning, yet we demonstrate that it is closely connected to learnability. In the computationally unbounded setting, we use a voting algorithm of Hanneke et al. (2022) to show that defendability is essentially determined by the VC dimension of the function class, in much the same way as PAC learnability. In the computationally bounded setting, we use a similar argument to show that efficient PAC learnability implies efficient defendability, but not conversely. On the other hand, we use indistinguishability obfuscation to show that the class of polynomial size circuits is not efficiently defendable. Finally, we present polynomial size decision trees as a natural example for which defense is strictly easier than learning. Thus, we identify efficient defendability as a notable intermediate concept in between efficient learnability and obfuscation.

Formalizing the presumption of independence

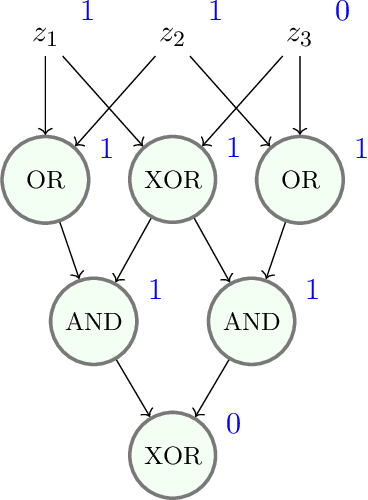
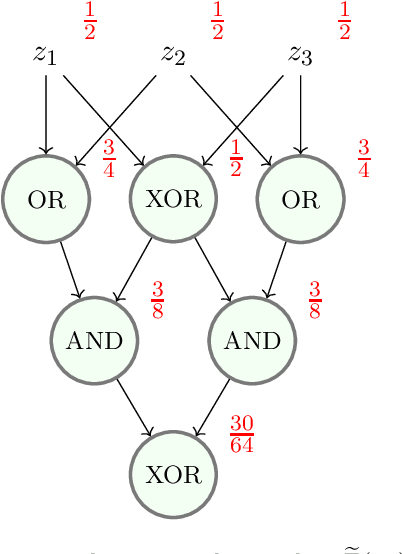
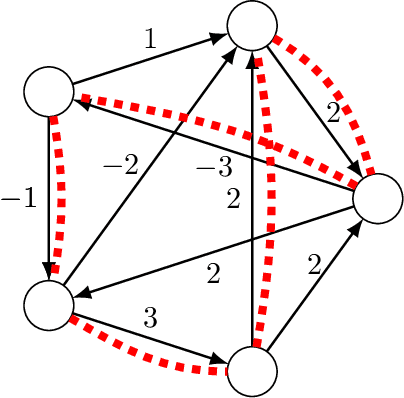
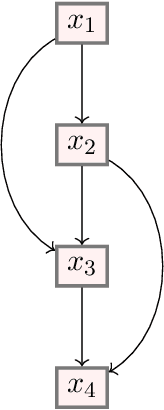
Mathematical proof aims to deliver confident conclusions, but a very similar process of deduction can be used to make uncertain estimates that are open to revision. A key ingredient in such reasoning is the use of a "default" estimate of $\mathbb{E}[XY] = \mathbb{E}[X] \mathbb{E}[Y]$ in the absence of any specific information about the correlation between $X$ and $Y$, which we call *the presumption of independence*. Reasoning based on this heuristic is commonplace, intuitively compelling, and often quite successful -- but completely informal. In this paper we introduce the concept of a heuristic estimator as a potential formalization of this type of defeasible reasoning. We introduce a set of intuitively desirable coherence properties for heuristic estimators that are not satisfied by any existing candidates. Then we present our main open problem: is there a heuristic estimator that formalizes intuitively valid applications of the presumption of independence without also accepting spurious arguments?