Backdoor defense, learnability and obfuscation
Paper and Code
Sep 04, 2024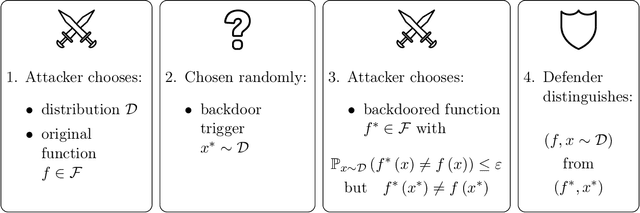
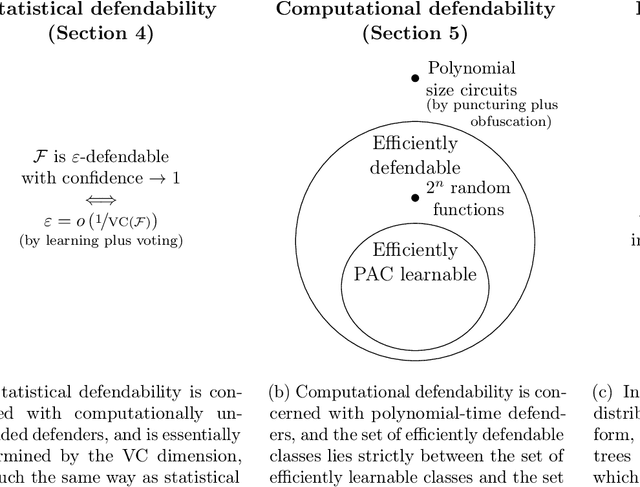
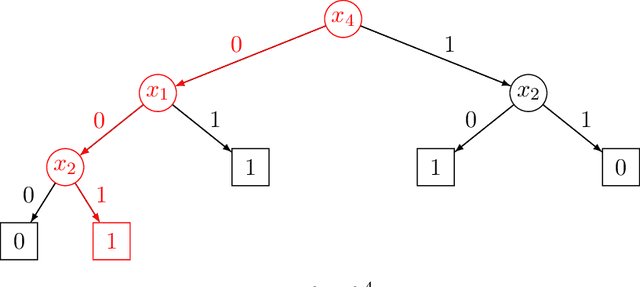
We introduce a formal notion of defendability against backdoors using a game between an attacker and a defender. In this game, the attacker modifies a function to behave differently on a particular input known as the "trigger", while behaving the same almost everywhere else. The defender then attempts to detect the trigger at evaluation time. If the defender succeeds with high enough probability, then the function class is said to be defendable. The key constraint on the attacker that makes defense possible is that the attacker's strategy must work for a randomly-chosen trigger. Our definition is simple and does not explicitly mention learning, yet we demonstrate that it is closely connected to learnability. In the computationally unbounded setting, we use a voting algorithm of Hanneke et al. (2022) to show that defendability is essentially determined by the VC dimension of the function class, in much the same way as PAC learnability. In the computationally bounded setting, we use a similar argument to show that efficient PAC learnability implies efficient defendability, but not conversely. On the other hand, we use indistinguishability obfuscation to show that the class of polynomial size circuits is not efficiently defendable. Finally, we present polynomial size decision trees as a natural example for which defense is strictly easier than learning. Thus, we identify efficient defendability as a notable intermediate concept in between efficient learnability and obfuscation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge