Formalizing the presumption of independence
Paper and Code
Nov 12, 2022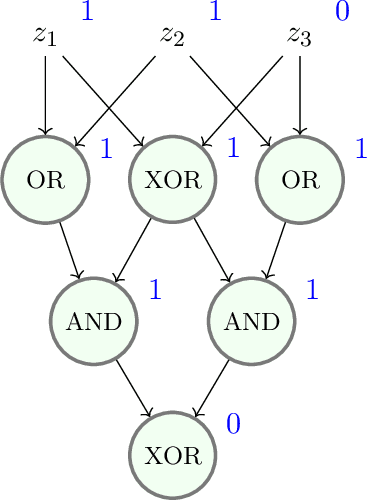
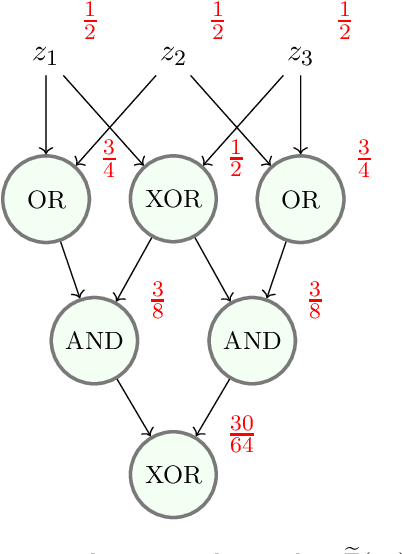
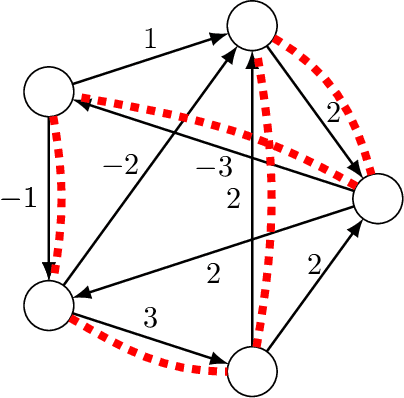
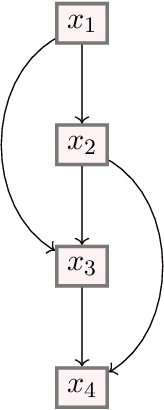
Mathematical proof aims to deliver confident conclusions, but a very similar process of deduction can be used to make uncertain estimates that are open to revision. A key ingredient in such reasoning is the use of a "default" estimate of $\mathbb{E}[XY] = \mathbb{E}[X] \mathbb{E}[Y]$ in the absence of any specific information about the correlation between $X$ and $Y$, which we call *the presumption of independence*. Reasoning based on this heuristic is commonplace, intuitively compelling, and often quite successful -- but completely informal. In this paper we introduce the concept of a heuristic estimator as a potential formalization of this type of defeasible reasoning. We introduce a set of intuitively desirable coherence properties for heuristic estimators that are not satisfied by any existing candidates. Then we present our main open problem: is there a heuristic estimator that formalizes intuitively valid applications of the presumption of independence without also accepting spurious arguments?
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge