Towards a Law of Iterated Expectations for Heuristic Estimators

Christiano et al. (2022) define a *heuristic estimator* to be a hypothetical algorithm that estimates the values of mathematical expressions from arguments. In brief, a heuristic estimator $\mathbb{G}$ takes as input a mathematical expression $Y$ and a formal "heuristic argument" $\pi$, and outputs an estimate $\mathbb{G}(Y \mid \pi)$ of $Y$. In this work, we argue for the informal principle that a heuristic estimator ought not to be able to predict its own errors, and we explore approaches to formalizing this principle. Most simply, the principle suggests that $\mathbb{G}(Y - \mathbb{G}(Y \mid \pi) \mid \pi)$ ought to equal zero for all $Y$ and $\pi$. We argue that an ideal heuristic estimator ought to satisfy two stronger properties in this vein, which we term *iterated estimation* (by analogy to the law of iterated expectations) and *error orthogonality*. Although iterated estimation and error orthogonality are intuitively appealing, it can be difficult to determine whether a given heuristic estimator satisfies the properties. As an alternative approach, we explore *accuracy*: a property that (roughly) states that $\mathbb{G}$ has zero average error over a distribution of mathematical expressions. However, in the context of two estimation problems, we demonstrate barriers to creating an accurate heuristic estimator. We finish by discussing challenges and potential paths forward for finding a heuristic estimator that accords with our intuitive understanding of how such an estimator ought to behave, as well as the potential applications of heuristic estimators to understanding the behavior of neural networks.

Algorithmic Bayesian Epistemology

One aspect of the algorithmic lens in theoretical computer science is a view on other scientific disciplines that focuses on satisfactory solutions that adhere to real-world constraints, as opposed to solutions that would be optimal ignoring such constraints. The algorithmic lens has provided a unique and important perspective on many academic fields, including molecular biology, ecology, neuroscience, quantum physics, economics, and social science. This thesis applies the algorithmic lens to Bayesian epistemology. Traditional Bayesian epistemology provides a comprehensive framework for how an individual's beliefs should evolve upon receiving new information. However, these methods typically assume an exhaustive model of such information, including the correlation structure between different pieces of evidence. In reality, individuals might lack such an exhaustive model, while still needing to form beliefs. Beyond such informational constraints, an individual may be bounded by limited computation, or by limited communication with agents that have access to information, or by the strategic behavior of such agents. Even when these restrictions prevent the formation of a *perfectly* accurate belief, arriving at a *reasonably* accurate belief remains crucial. In this thesis, we establish fundamental possibility and impossibility results about belief formation under a variety of restrictions, and lay the groundwork for further exploration.

Formalizing the presumption of independence

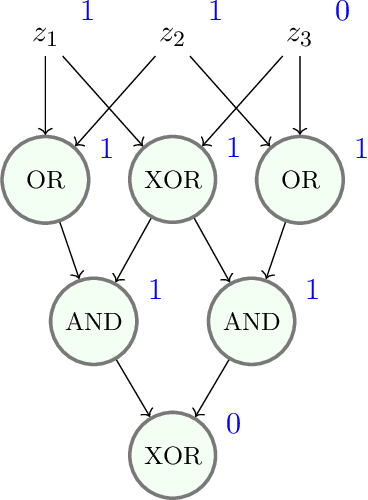
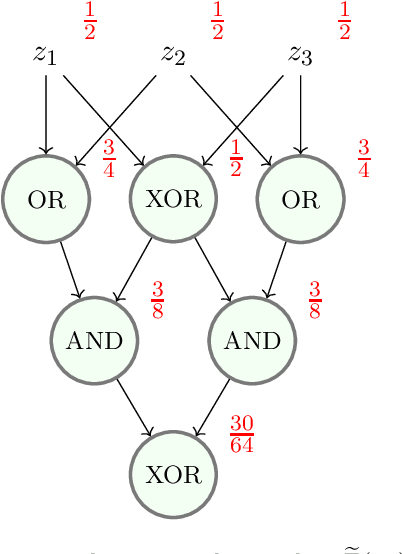
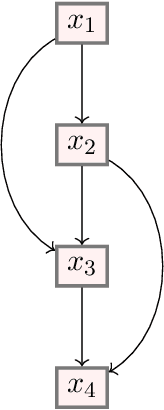
Mathematical proof aims to deliver confident conclusions, but a very similar process of deduction can be used to make uncertain estimates that are open to revision. A key ingredient in such reasoning is the use of a "default" estimate of $\mathbb{E}[XY] = \mathbb{E}[X] \mathbb{E}[Y]$ in the absence of any specific information about the correlation between $X$ and $Y$, which we call *the presumption of independence*. Reasoning based on this heuristic is commonplace, intuitively compelling, and often quite successful -- but completely informal. In this paper we introduce the concept of a heuristic estimator as a potential formalization of this type of defeasible reasoning. We introduce a set of intuitively desirable coherence properties for heuristic estimators that are not satisfied by any existing candidates. Then we present our main open problem: is there a heuristic estimator that formalizes intuitively valid applications of the presumption of independence without also accepting spurious arguments?

No-Regret Learning with Unbounded Losses: The Case of Logarithmic Pooling

For each of $T$ time steps, $m$ experts report probability distributions over $n$ outcomes; we wish to learn to aggregate these forecasts in a way that attains a no-regret guarantee. We focus on the fundamental and practical aggregation method known as logarithmic pooling -- a weighted average of log odds -- which is in a certain sense the optimal choice of pooling method if one is interested in minimizing log loss (as we take to be our loss function). We consider the problem of learning the best set of parameters (i.e. expert weights) in an online adversarial setting. We assume (by necessity) that the adversarial choices of outcomes and forecasts are consistent, in the sense that experts report calibrated forecasts. Our main result is an algorithm based on online mirror descent that learns expert weights in a way that attains $O(\sqrt{T} \log T)$ expected regret as compared with the best weights in hindsight.

Are You Smarter Than a Random Expert? The Robust Aggregation of Substitutable Signals

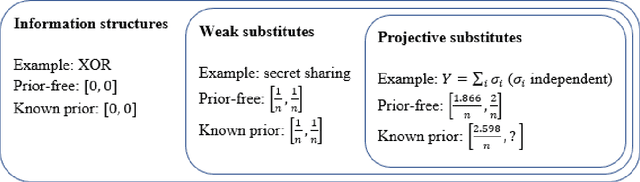
The problem of aggregating expert forecasts is ubiquitous in fields as wide-ranging as machine learning, economics, climate science, and national security. Despite this, our theoretical understanding of this question is fairly shallow. This paper initiates the study of forecast aggregation in a context where experts' knowledge is chosen adversarially from a broad class of information structures. While in full generality it is impossible to achieve a nontrivial performance guarantee, we show that doing so is possible under a condition on the experts' information structure that we call \emph{projective substitutes}. The projective substitutes condition is a notion of informational substitutes: that there are diminishing marginal returns to learning the experts' signals. We show that under the projective substitutes condition, taking the average of the experts' forecasts improves substantially upon the strategy of trusting a random expert. We then consider a more permissive setting, in which the aggregator has access to the prior. We show that by averaging the experts' forecasts and then \emph{extremizing} the average by moving it away from the prior by a constant factor, the aggregator's performance guarantee is substantially better than is possible without knowledge of the prior. Our results give a theoretical grounding to past empirical research on extremization and help give guidance on the appropriate amount to extremize.