Feature Network Methods in Machine Learning and Applications

A machine learning (ML) feature network is a graph that connects ML features in learning tasks based on their similarity. This network representation allows us to view feature vectors as functions on the network. By leveraging function operations from Fourier analysis and from functional analysis, one can easily generate new and novel features, making use of the graph structure imposed on the feature vectors. Such network structures have previously been studied implicitly in image processing and computational biology. We thus describe feature networks as graph structures imposed on feature vectors, and provide applications in machine learning. One application involves graph-based generalizations of convolutional neural networks, involving structured deep learning with hierarchical representations of features that have varying depth or complexity. This extends also to learning algorithms that are able to generate useful new multilevel features. Additionally, we discuss the use of feature networks to engineer new features, which can enhance the expressiveness of the model. We give a specific example of a deep tree-structured feature network, where hierarchical connections are formed through feature clustering and feed-forward learning. This results in low learning complexity and computational efficiency. Unlike "standard" neural features which are limited to modulated (thresholded) linear combinations of adjacent ones, feature networks offer more general feedforward dependencies among features. For example, radial basis functions or graph structure-based dependencies between features can be utilized.

Stochastic Functional Analysis and Multilevel Vector Field Anomaly Detection

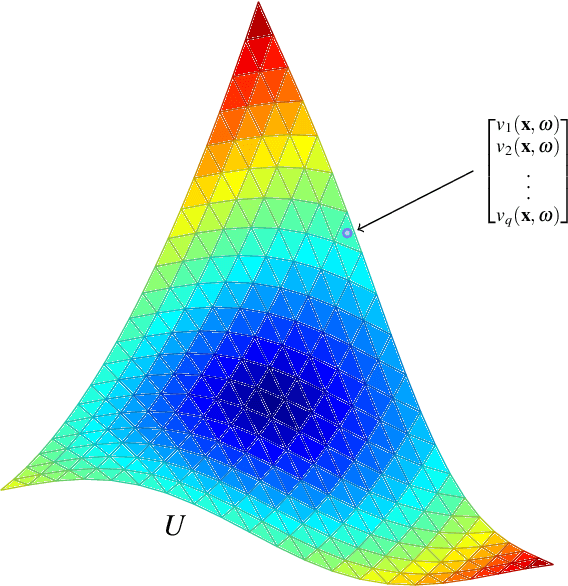
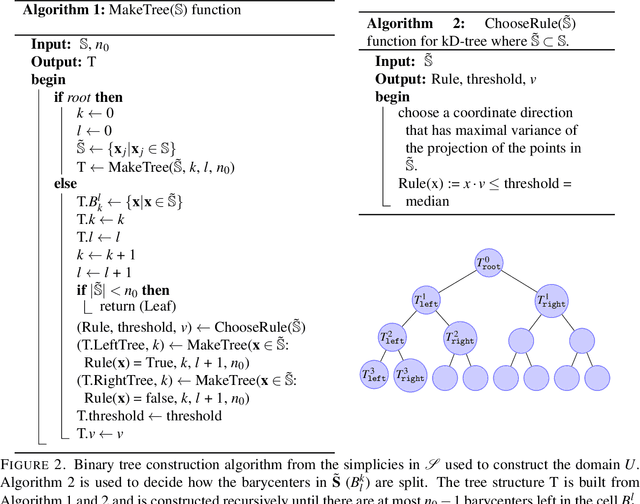
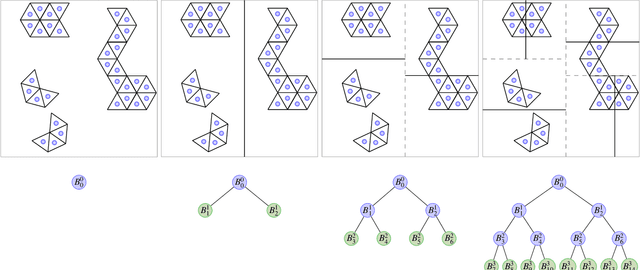
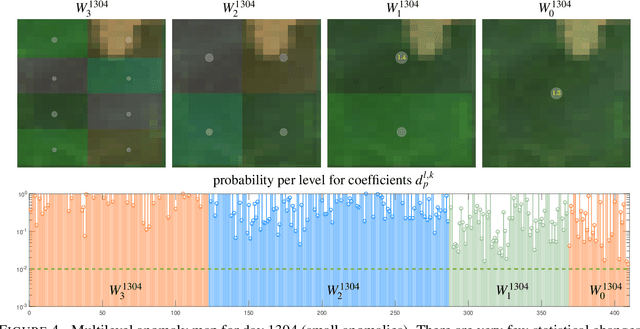
Massive vector field datasets are common in multi-spectral optical and radar sensors and modern multimodal MRI data, among many other areas of application. In this paper we develop a novel stochastic functional analysis approach for detecting anomalies based on the covariance structure of nominal stochastic behavior across a domain with multi-band vector field data. An optimal vector field Karhunen-Loeve (KL) expansion is applied to such random field data. A series of multilevel orthogonal functional subspaces is constructed from the geometry of the domain, adapted from the KL expansion. Detection is achieved by examining the projection of the random field on the multilevel basis. The anomalies can be quantified in suitable normed spaces based on local and global information. In addition, reliable hypothesis tests are formed with controllable distributions that do not require prior assumptions on probability distributions of the data. Only the covariance function is needed, which makes for significantly simpler estimates. Furthermore this approach allows stochastic vector-based fusion of anomalies without any loss of information. The method is applied to the important problem of deforestation and degradation in the Amazon forest. This is a complex non-monotonic process, as forests can degrade and recover. This particular problem is further compounded by the presence of clouds that are hard to remove with current masking algorithms. Using multi-spectral satellite data from Sentinel 2, the multilevel filter is constructed and anomalies are treated as deviations from the initial state of the forest. Forest anomalies are quantified with robust hypothesis tests and distinguished from false variations such as cloud cover. Our approach shows the advantage of using multiple bands of data in a vectorized complex, leading to better anomaly detection beyond the capabilities of scalar-based methods.

Multilevel Stochastic Optimization for Imputation in Massive Medical Data Records

Exploration and analysis of massive datasets has recently generated increasing interest in the research and development communities. It has long been a recognized problem that many datasets contain significant levels of missing numerical data. We introduce a mathematically principled stochastic optimization imputation method based on the theory of Kriging. This is shown to be a powerful method for imputation. However, its computational effort and potential numerical instabilities produce costly and/or unreliable predictions, potentially limiting its use on large scale datasets. In this paper, we apply a recently developed multi-level stochastic optimization approach to the problem of imputation in massive medical records. The approach is based on computational applied mathematics techniques and is highly accurate. In particular, for the Best Linear Unbiased Predictor (BLUP) this multi-level formulation is exact, and is also significantly faster and more numerically stable. This permits practical application of Kriging methods to data imputation problems for massive datasets. We test this approach on data from the National Inpatient Sample (NIS) data records, Healthcare Cost and Utilization Project (HCUP), Agency for Healthcare Research and Quality. Numerical results show the multi-level method significantly outperforms current approaches and is numerically robust. In particular, it has superior accuracy as compared with methods recommended in the recent report from HCUP on the important problem of missing data, which could lead to sub-optimal and poorly based funding policy decisions. In comparative benchmark tests it is shown that the multilevel stochastic method is significantly superior to recommended methods in the report, including Predictive Mean Matching (PMM) and Predicted Posterior Distribution (PPD), with up to 75% reductions in error.

Stochastic functional analysis with applications to robust machine learning

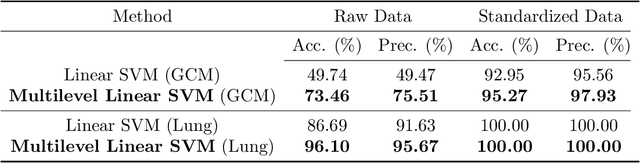
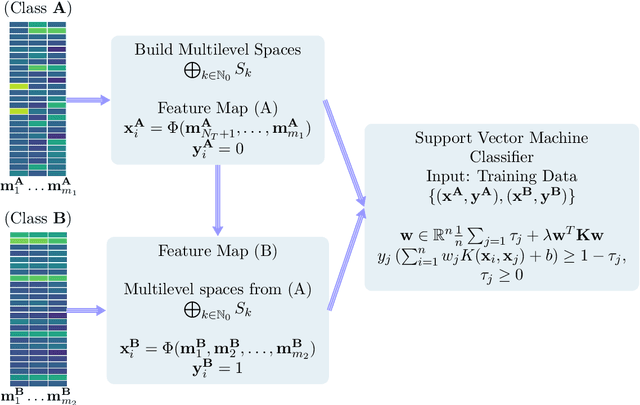
It is well-known that machine learning protocols typically under-utilize information on the probability distributions of feature vectors and related data, and instead directly compute regression or classification functions of feature vectors. In this paper we introduce a set of novel features for identifying underlying stochastic behavior of input data using the Karhunen-Lo\'{e}ve (KL) expansion, where classification is treated as detection of anomalies from a (nominal) signal class. These features are constructed from the recent Functional Data Analysis (FDA) theory for anomaly detection. The related signal decomposition is an exact hierarchical tensor product expansion with known optimality properties for approximating stochastic processes (random fields) with finite dimensional function spaces. In principle these primary low dimensional spaces can capture most of the stochastic behavior of `underlying signals' in a given nominal class, and can reject signals in alternative classes as stochastic anomalies. Using a hierarchical finite dimensional KL expansion of the nominal class, a series of orthogonal nested subspaces is constructed for detecting anomalous signal components. Projection coefficients of input data in these subspaces are then used to train an ML classifier. However, due to the split of the signal into nominal and anomalous projection components, clearer separation surfaces of the classes arise. In fact we show that with a sufficiently accurate estimation of the covariance structure of the nominal class, a sharp classification can be obtained. We carefully formulate this concept and demonstrate it on a number of high-dimensional datasets in cancer diagnostics. This method leads to a significant increase in precision and accuracy over the current top benchmarks for the Global Cancer Map (GCM) gene expression network dataset.

Feature vector regularization in machine learning

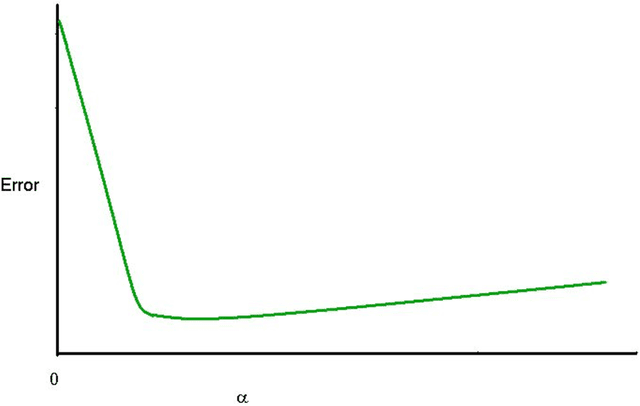
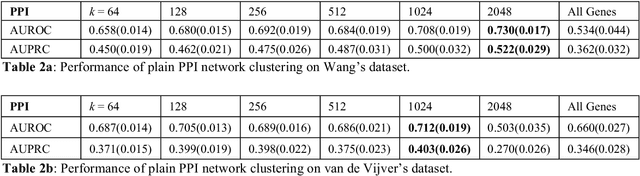
Problems in machine learning (ML) can involve noisy input data, and ML classification methods have reached limiting accuracies when based on standard ML data sets consisting of feature vectors and their classes. Greater accuracy will require incorporation of prior structural information on data into learning. We study methods to regularize feature vectors (unsupervised regularization methods), analogous to supervised regularization for estimating functions in ML. We study regularization (denoising) of ML feature vectors using Tikhonov and other regularization methods for functions on ${\bf R}^n$. A feature vector ${\bf x}=(x_1,\ldots,x_n)=\{x_q\}_{q=1}^n$ is viewed as a function of its index $q$, and smoothed using prior information on its structure. This can involve a penalty functional on feature vectors analogous to those in statistical learning, or use of proximity (e.g. graph) structure on the set of indices. Such feature vector regularization inherits a property from function denoising on ${\bf R}^n$, in that accuracy is non-monotonic in the denoising (regularization) parameter $\alpha$. Under some assumptions about the noise level and the data structure, we show that the best reconstruction accuracy also occurs at a finite positive $\alpha$ in index spaces with graph structures. We adapt two standard function denoising methods used on ${\bf R}^n$, local averaging and kernel regression. In general the index space can be any discrete set with a notion of proximity, e.g. a metric space, a subset of ${\bf R}^n$, or a graph/network, with feature vectors as functions with some notion of continuity. We show this improves feature vector recovery, and thus the subsequent classification or regression done on them. We give an example in gene expression analysis for cancer classification with the genome as an index space and network structure based protein-protein interactions.