Stochastic Functional Analysis and Multilevel Vector Field Anomaly Detection

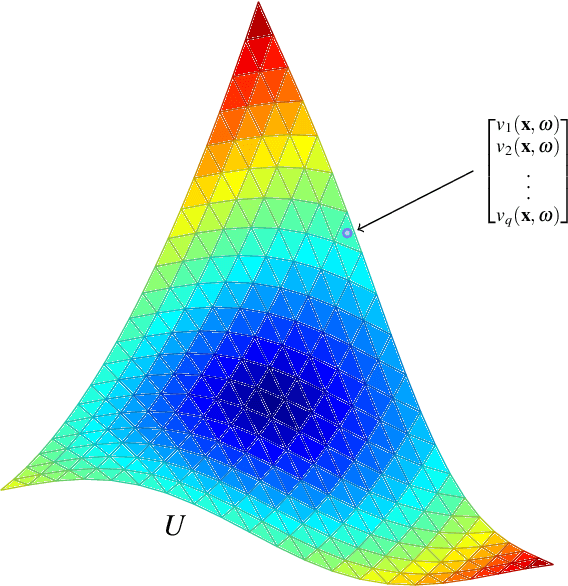
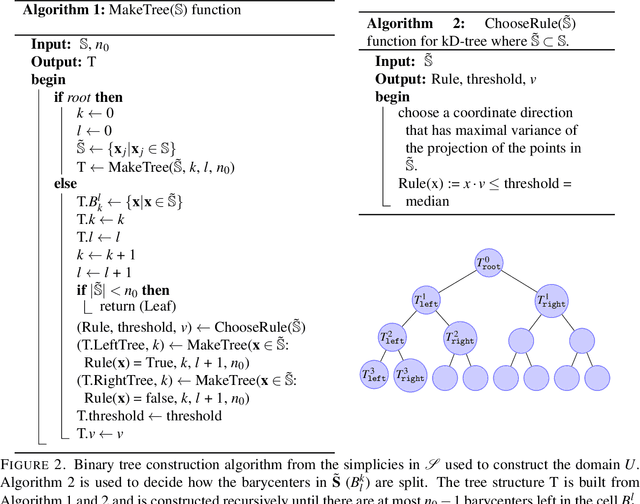
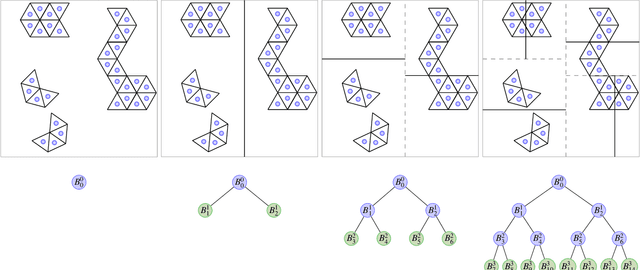
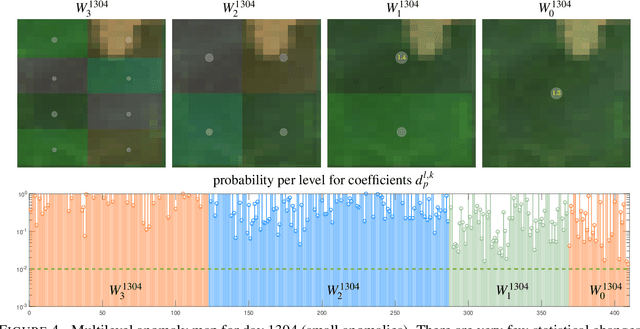
Massive vector field datasets are common in multi-spectral optical and radar sensors and modern multimodal MRI data, among many other areas of application. In this paper we develop a novel stochastic functional analysis approach for detecting anomalies based on the covariance structure of nominal stochastic behavior across a domain with multi-band vector field data. An optimal vector field Karhunen-Loeve (KL) expansion is applied to such random field data. A series of multilevel orthogonal functional subspaces is constructed from the geometry of the domain, adapted from the KL expansion. Detection is achieved by examining the projection of the random field on the multilevel basis. The anomalies can be quantified in suitable normed spaces based on local and global information. In addition, reliable hypothesis tests are formed with controllable distributions that do not require prior assumptions on probability distributions of the data. Only the covariance function is needed, which makes for significantly simpler estimates. Furthermore this approach allows stochastic vector-based fusion of anomalies without any loss of information. The method is applied to the important problem of deforestation and degradation in the Amazon forest. This is a complex non-monotonic process, as forests can degrade and recover. This particular problem is further compounded by the presence of clouds that are hard to remove with current masking algorithms. Using multi-spectral satellite data from Sentinel 2, the multilevel filter is constructed and anomalies are treated as deviations from the initial state of the forest. Forest anomalies are quantified with robust hypothesis tests and distinguished from false variations such as cloud cover. Our approach shows the advantage of using multiple bands of data in a vectorized complex, leading to better anomaly detection beyond the capabilities of scalar-based methods.