Stochastic functional analysis with applications to robust machine learning

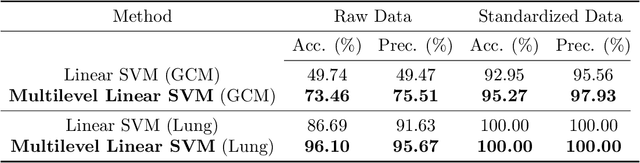
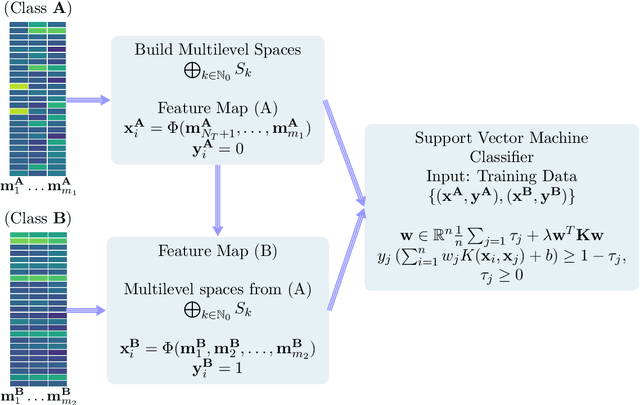
It is well-known that machine learning protocols typically under-utilize information on the probability distributions of feature vectors and related data, and instead directly compute regression or classification functions of feature vectors. In this paper we introduce a set of novel features for identifying underlying stochastic behavior of input data using the Karhunen-Lo\'{e}ve (KL) expansion, where classification is treated as detection of anomalies from a (nominal) signal class. These features are constructed from the recent Functional Data Analysis (FDA) theory for anomaly detection. The related signal decomposition is an exact hierarchical tensor product expansion with known optimality properties for approximating stochastic processes (random fields) with finite dimensional function spaces. In principle these primary low dimensional spaces can capture most of the stochastic behavior of `underlying signals' in a given nominal class, and can reject signals in alternative classes as stochastic anomalies. Using a hierarchical finite dimensional KL expansion of the nominal class, a series of orthogonal nested subspaces is constructed for detecting anomalous signal components. Projection coefficients of input data in these subspaces are then used to train an ML classifier. However, due to the split of the signal into nominal and anomalous projection components, clearer separation surfaces of the classes arise. In fact we show that with a sufficiently accurate estimation of the covariance structure of the nominal class, a sharp classification can be obtained. We carefully formulate this concept and demonstrate it on a number of high-dimensional datasets in cancer diagnostics. This method leads to a significant increase in precision and accuracy over the current top benchmarks for the Global Cancer Map (GCM) gene expression network dataset.