Mario Coutino
Revisiting Matching Pursuit: Beyond Approximate Submodularity
May 12, 2023



Abstract:We study the problem of selecting a subset of vectors from a large set, to obtain the best signal representation over a family of functions. Although greedy methods have been widely used for tackling this problem and many of those have been analyzed under the lens of (weak) submodularity, none of these algorithms are explicitly devised using such a functional property. Here, we revisit the vector-selection problem and introduce a function which is shown to be submodular in expectation. This function does not only guarantee near-optimality through a greedy algorithm in expectation, but also alleviates the existing deficiencies in commonly used matching pursuit (MP) algorithms. We further show the relation between the single-point-estimate version of the proposed greedy algorithm and MP variants. Our theoretical results are supported by numerical experiments for the angle of arrival estimation problem, a typical signal representation task; the experiments demonstrate the benefits of the proposed method with respect to the traditional MP algorithms.
Run-Time Monitors Design for Adaptive Radar Systems: A Practical Framework
Feb 20, 2023Abstract:Adaptivity in multi-function radar systems is rapidly increasing, especially when moving towards fully adaptive, cognitive radar systems. However, the large number of available system configurations makes the rigorous verification and certification process during the testing phase, deployment, and after hardware and software upgrades, challenging, if not infeasible. To alleviate the verification process, run-time verification can be applied to oversee the correct function of a system during its operation as done in applications where on-the-fly reconfiguration/adaptation is pervasive, e.g., spacecrafts and self-driving cars. Though possible, the application of run-time verification into a radar system is not straightforward, e.g., when verifying (adaptive) radar resource managers or performance measures, such as track initiation time in dynamic environments. The goal of this paper is to introduce a framework to identify, characterize, and map the various aspects necessary for implementing run-time verification for (components of) multi-function radar systems. The proposed framework can be used by radar practitioners and researchers for applying run-time-verification to adaptive, re-configurable radar systems. In addition, we discuss how run-time verification can be leveraged to gather new insights from operational data to improve functionalities in upcoming update cycles and present an example of a verifier designed using the introduced framework.
Learning Time-Varying Graphs from Online Data
Oct 21, 2021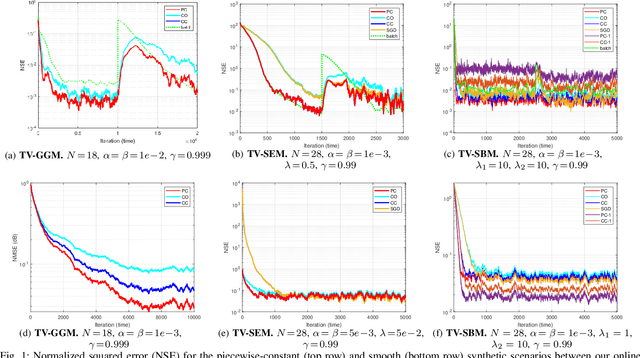
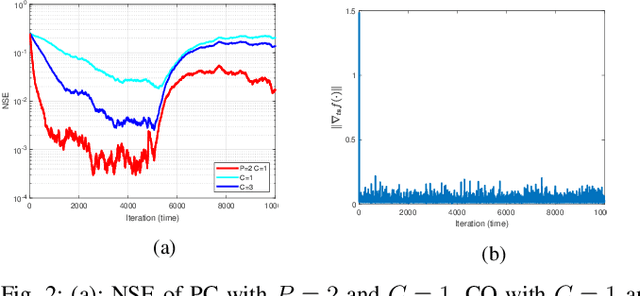
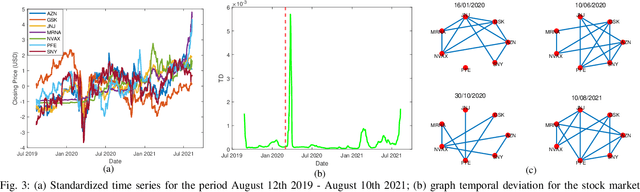
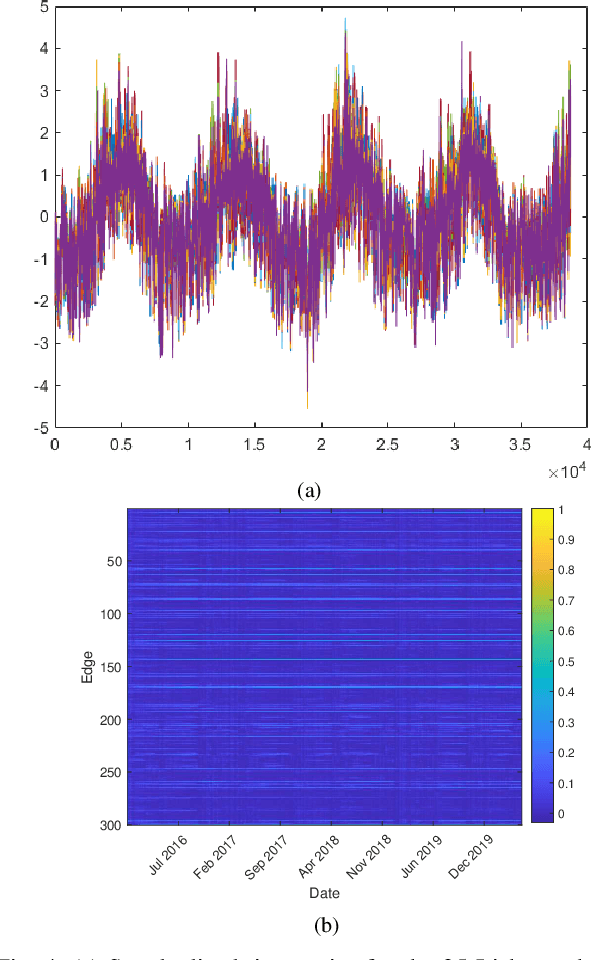
Abstract:This work proposes an algorithmic framework to learn time-varying graphs from online data. The generality offered by the framework renders it model-independent, i.e., it can be theoretically analyzed in its abstract formulation and then instantiated under a variety of model-dependent graph learning problems. This is possible by phrasing (time-varying) graph learning as a composite optimization problem, where different functions regulate different desiderata, e.g., data fidelity, sparsity or smoothness. Instrumental for the findings is recognizing that the dependence of the majority (if not all) data-driven graph learning algorithms on the data is exerted through the empirical covariance matrix, representing a sufficient statistic for the estimation problem. Its user-defined recursive update enables the framework to work in non-stationary environments, while iterative algorithms building on novel time-varying optimization tools explicitly take into account the temporal dynamics, speeding up convergence and implicitly including a temporal-regularization of the solution. We specialize the framework to three well-known graph learning models, namely, the Gaussian graphical model (GGM), the structural equation model (SEM), and the smoothness-based model (SBM), where we also introduce ad-hoc vectorization schemes for structured matrices (symmetric, hollows, etc.) which are crucial to perform correct gradient computations, other than enabling to work in low-dimensional vector spaces and hence easing storage requirements. After discussing the theoretical guarantees of the proposed framework, we corroborate it with extensive numerical tests in synthetic and real data.
Online Time-Varying Topology Identification via Prediction-Correction Algorithms
Oct 22, 2020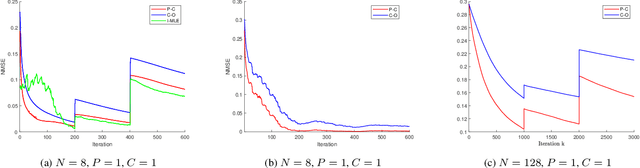
Abstract:Signal processing and machine learning algorithms for data supported over graphs, require the knowledge of the graph topology. Unless this information is given by the physics of the problem (e.g., water supply networks, power grids), the topology has to be learned from data. Topology identification is a challenging task, as the problem is often ill-posed, and becomes even harder when the graph structure is time-varying. In this paper, we address the problem of dynamic topology identification by building on recent results from time-varying optimization, devising a general-purpose online algorithm operating in non-stationary environments. Because of its iteration-constrained nature, the proposed approach exhibits an intrinsic temporal-regularization of the graph topology without explicitly enforcing it. As a case-study, we specialize our method to the Gaussian graphical model (GGM) problem and corroborate its performance.
How Does Momentum Help Frank Wolfe?
Jun 19, 2020



Abstract:We unveil the connections between Frank Wolfe (FW) type algorithms and the momentum in Accelerated Gradient Methods (AGM). On the negative side, these connections illustrate why momentum is unlikely to be effective for FW type algorithms. The encouraging message behind this link, on the other hand, is that momentum is useful for FW on a class of problems. In particular, we prove that a momentum variant of FW, that we term accelerated Frank Wolfe (AFW), converges with a faster rate $\tilde{\cal O}(\frac{1}{k^2})$ on certain constraint sets despite the same ${\cal O}(\frac{1}{k})$ rate as FW on general cases. Given the possible acceleration of AFW at almost no extra cost, it is thus a competitive alternative to FW. Numerical experiments on benchmarked machine learning tasks further validate our theoretical findings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge