Realistic noise synthesis reduces bias and improves tissue microstructure estimation with supervised machine learning

Diffusion MRI enables non-invasive probing of tissue microstructure, but accurate parameter estimation is challenged by noise-related effects. In supervised machine learning frameworks trained on simulated data, discrepancies between the noise characteristics of simulated and acquired signals introduce a form of covariate shift, whereby the input signal distribution differs between training and inference. We investigated the impact of this mismatch on microstructure parameter estimation and propose a realistic noise synthesis (RNS) framework to mitigate it. RNS incorporates both the Rician expectation and the effective post-processing noise variance into simulated training signals. The Rician expectation was modelled using a noise standard deviation estimated with MPPCA, while the effective standard deviation was derived from spherical harmonic residuals of preprocessed data. The method was evaluated using the cylinder-zeppelin and the SANDI models on simulated datasets across multiple SNR levels and on in vivo diffusion data with repeated acquisitions. Sensitivity to noise misestimation was also assessed. Ignoring magnitude-induced noise effects during training produced systematic, SNR-dependent parameter bias, particularly at low SNR. Incorporating the Rician expectation substantially reduced bias to the level of noise-aware nonlinear least-squares fitting. Modelling the effective standard deviation further improved precision. Performance was largely independent of regression architecture but sensitive to accurate noise estimation. These findings demonstrate that realistic noise modelling in simulated training data mitigates signal-domain covariate shift and is essential for unbiased supervised microstructure estimation, particularly in low-SNR regimes associated with high b-values or high spatial resolution.

Shining light on degeneracies and uncertainties in quantifying both exchange and restriction with time-dependent diffusion MRI using Bayesian inference

Diffusion MRI (dMRI) biophysical models hold promise for characterizing gray matter tissue microstructure. Yet, the reliability of estimated parameters remains largely under-studied, especially in models that incorporate water exchange. In this study, we investigate the accuracy, precision, and presence of degeneracy of two recently proposed gray matter models, NEXI and SANDIX, using two acquisition protocols from the literature, on both simulated and in vivo data. We employ $\mu$GUIDE, a Bayesian inference framework based on deep learning, to quantify model uncertainty and detect parameter degeneracies, enabling a more interpretable assessment of fitted parameters. Our results show that while some microstructural parameters, such as extra-cellular diffusivity and neurite signal fraction, are robustly estimated, others, such as exchange time and soma radius, are often associated with high uncertainty and estimation bias, especially under realistic noise conditions and reduced acquisition protocols. Comparisons with non-linear least squares fitting underscore the added value of uncertainty-aware methods, which allow for the identification and filtering of unreliable estimates. These findings emphasize the need to report uncertainty and consider model degeneracies when interpreting model-based estimates. Our study advocates for the integration of probabilistic fitting approaches in neuroscience imaging pipelines to improve reproducibility and biological interpretability.

Image Quality Transfer of Diffusion MRI Guided By High-Resolution Structural MRI

Prior work on the Image Quality Transfer on Diffusion MRI (dMRI) has shown significant improvement over traditional interpolation methods. However, the difficulty in obtaining ultra-high resolution Diffusion MRI scans poses a problem in training neural networks to obtain high-resolution dMRI scans. Here we hypothesise that the inclusion of structural MRI images, which can be acquired at much higher resolutions, can be used as a guide to obtaining a more accurate high-resolution dMRI output. To test our hypothesis, we have constructed a novel framework that incorporates structural MRI scans together with dMRI to obtain high-resolution dMRI scans. We set up tests which evaluate the validity of our claim through various configurations and compare the performance of our approach against a unimodal approach. Our results show that the inclusion of structural MRI scans do lead to an improvement in high-resolution image prediction when T1w data is incorporated into the model input.

$μ$GUIDE: a framework for microstructure imaging via generalized uncertainty-driven inference using deep learning

This work proposes $\mu$GUIDE: a general Bayesian framework to estimate posterior distributions of tissue microstructure parameters from any given biophysical model or MRI signal representation, with exemplar demonstration in diffusion-weighted MRI. Harnessing a new deep learning architecture for automatic signal feature selection combined with simulation-based inference and efficient sampling of the posterior distributions, $\mu$GUIDE bypasses the high computational and time cost of conventional Bayesian approaches and does not rely on acquisition constraints to define model-specific summary statistics. The obtained posterior distributions allow to highlight degeneracies present in the model definition and quantify the uncertainty and ambiguity of the estimated parameters.

Fitting a Directional Microstructure Model to Diffusion-Relaxation MRI Data with Self-Supervised Machine Learning

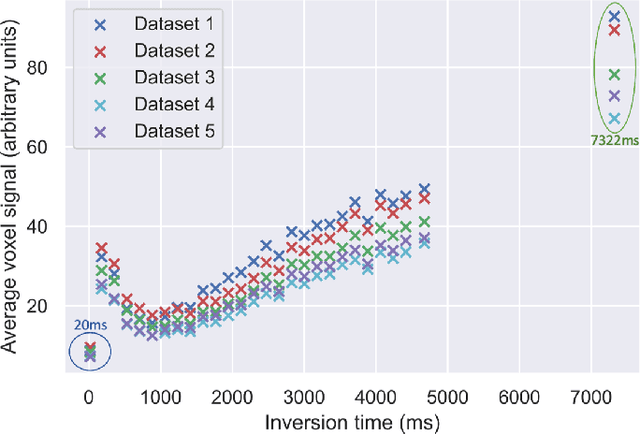
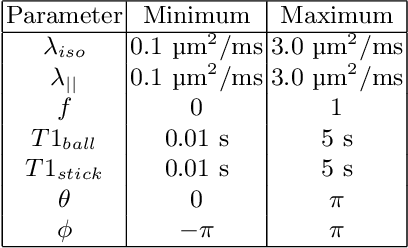
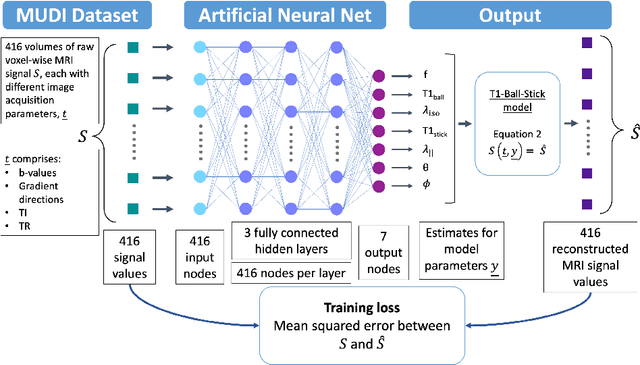
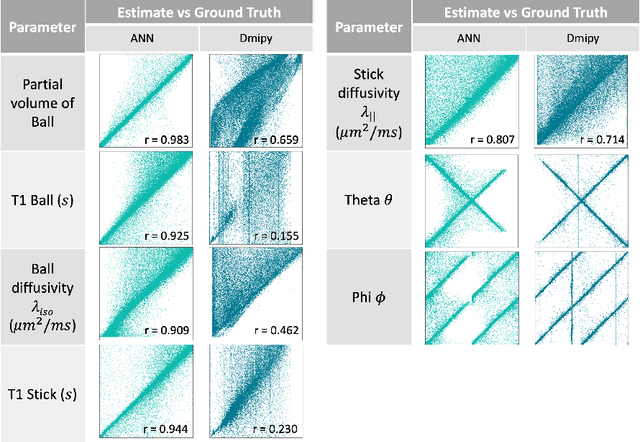
Machine learning is a powerful approach for fitting microstructural models to diffusion MRI data. Early machine learning microstructure imaging implementations trained regressors to estimate model parameters in a supervised way, using synthetic training data with known ground truth. However, a drawback of this approach is that the choice of training data impacts fitted parameter values. Self-supervised learning is emerging as an attractive alternative to supervised learning in this context. Thus far, both supervised and self-supervised learning have typically been applied to isotropic models, such as intravoxel incoherent motion (IVIM), as opposed to models where the directionality of anisotropic structures is also estimated. In this paper, we demonstrate self-supervised machine learning model fitting for a directional microstructural model. In particular, we fit a combined T1-ball-stick model to the multidimensional diffusion (MUDI) challenge diffusion-relaxation dataset. Our self-supervised approach shows clear improvements in parameter estimation and computational time, for both simulated and in-vivo brain data, compared to standard non-linear least squares fitting. Code for the artificial neural net constructed for this study is available for public use from the following GitHub repository: https://github.com/jplte/deep-T1-ball-stick

Lossy compression of multidimensional medical images using sinusoidal activation networks: an evaluation study

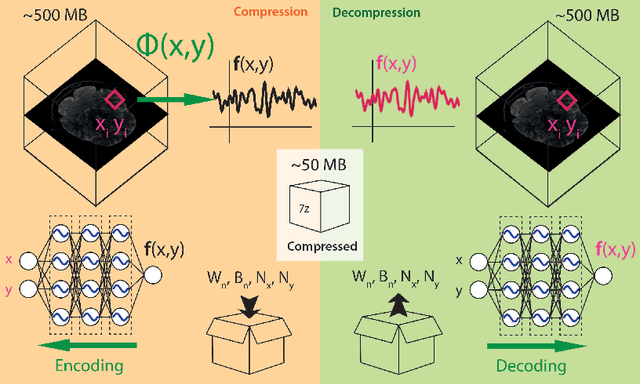
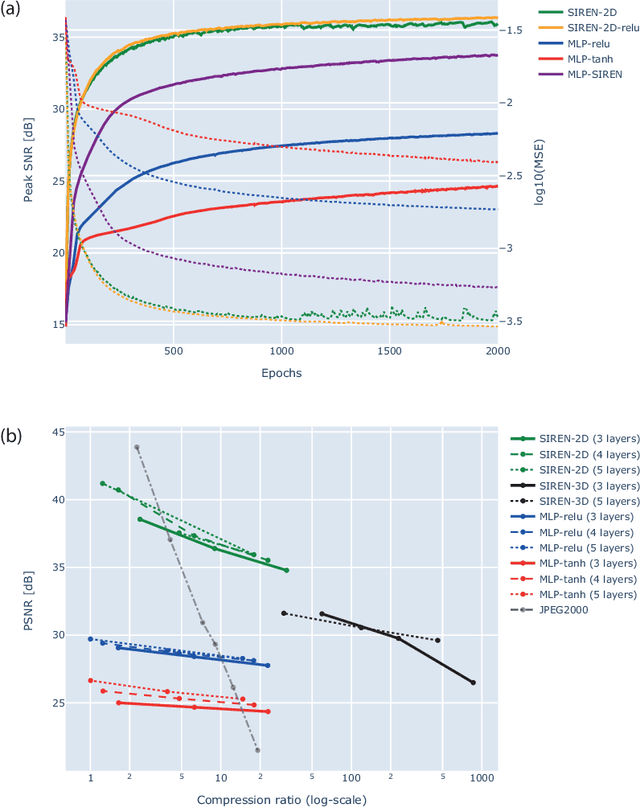
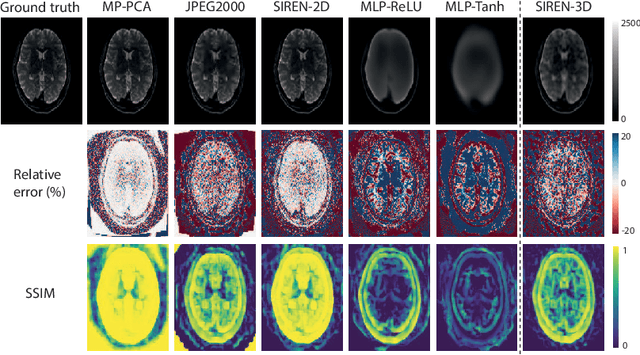
In this work, we evaluate how neural networks with periodic activation functions can be leveraged to reliably compress large multidimensional medical image datasets, with proof-of-concept application to 4D diffusion-weighted MRI (dMRI). In the medical imaging landscape, multidimensional MRI is a key area of research for developing biomarkers that are both sensitive and specific to the underlying tissue microstructure. However, the high-dimensional nature of these data poses a challenge in terms of both storage and sharing capabilities and associated costs, requiring appropriate algorithms able to represent the information in a low-dimensional space. Recent theoretical developments in deep learning have shown how periodic activation functions are a powerful tool for implicit neural representation of images and can be used for compression of 2D images. Here we extend this approach to 4D images and show how any given 4D dMRI dataset can be accurately represented through the parameters of a sinusoidal activation network, achieving a data compression rate about 10 times higher than the standard DEFLATE algorithm. Our results show that the proposed approach outperforms benchmark ReLU and Tanh activation perceptron architectures in terms of mean squared error, peak signal-to-noise ratio and structural similarity index. Subsequent analyses using the tensor and spherical harmonics representations demonstrate that the proposed lossy compression reproduces accurately the characteristics of the original data, leading to relative errors about 5 to 10 times lower than the benchmark JPEG2000 lossy compression and similar to standard pre-processing steps such as MP-PCA denosing, suggesting a loss of information within the currently accepted levels for clinical application.

Multi-Stage Prediction Networks for Data Harmonization

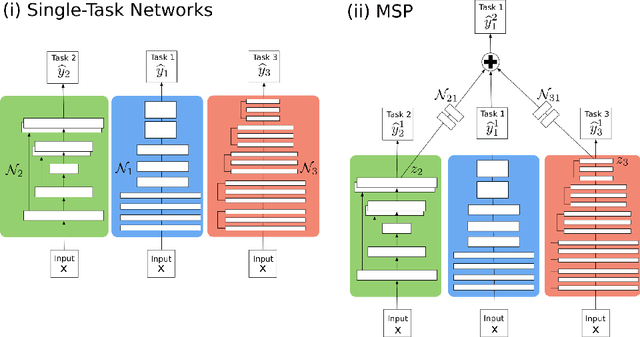
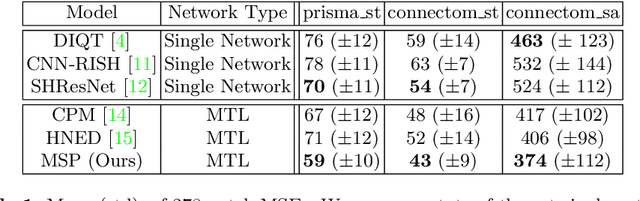
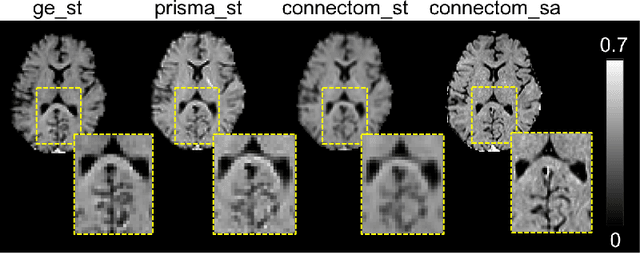
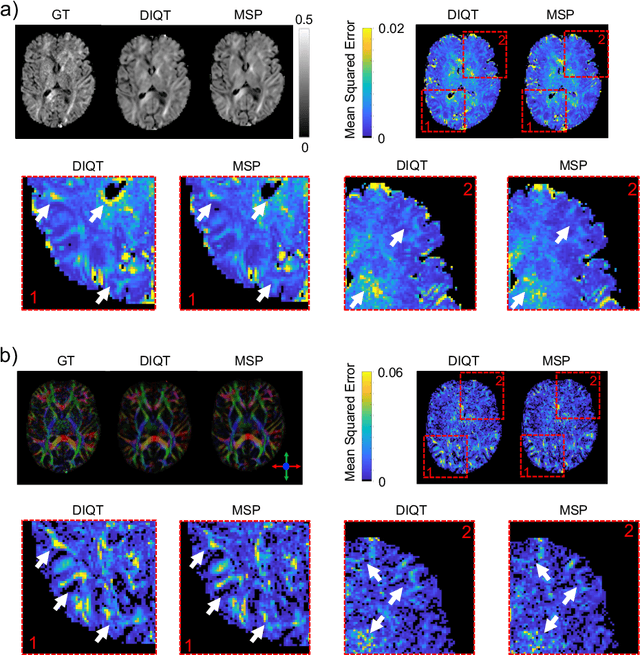
In this paper, we introduce multi-task learning (MTL) to data harmonization (DH); where we aim to harmonize images across different acquisition platforms and sites. This allows us to integrate information from multiple acquisitions and improve the predictive performance and learning efficiency of the harmonization model. Specifically, we introduce the Multi Stage Prediction (MSP) Network, a MTL framework that incorporates neural networks of potentially disparate architectures, trained for different individual acquisition platforms, into a larger architecture that is refined in unison. The MSP utilizes high-level features of single networks for individual tasks, as inputs of additional neural networks to inform the final prediction, therefore exploiting redundancy across tasks to make the most of limited training data. We validate our methods on a dMRI harmonization challenge dataset, where we predict three modern platform types, from one obtained from an old scanner. We show how MTL architectures, such as the MSP, produce around 20\% improvement of patch-based mean-squared error over current state-of-the-art methods and that our MSP outperforms off-the-shelf MTL networks. Our code is available https://github.com/sbb-gh/ .