Analytic Manifold Learning: Unifying and Evaluating Representations for Continuous Control

We address the problem of learning reusable state representations from streaming high-dimensional observations. This is important for areas like Reinforcement Learning (RL), which yields non-stationary data distributions during training. We make two key contributions. First, we propose an evaluation suite that measures alignment between latent and true low-dimensional states. We benchmark several widely used unsupervised learning approaches. This uncovers the strengths and limitations of existing approaches that impose additional constraints/objectives on the latent space. Our second contribution is a unifying mathematical formulation for learning latent relations. We learn analytic relations on source domains, then use these relations to help structure the latent space when learning on target domains. This formulation enables a more general, flexible and principled way of shaping the latent space. It formalizes the notion of learning independent relations, without imposing restrictive simplifying assumptions or requiring domain-specific information. We present mathematical properties, concrete algorithms for implementation and experimental validation of successful learning and transfer of latent relations.

Inability of spatial transformations of CNN feature maps to support invariant recognition

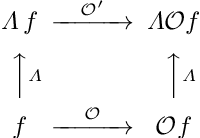
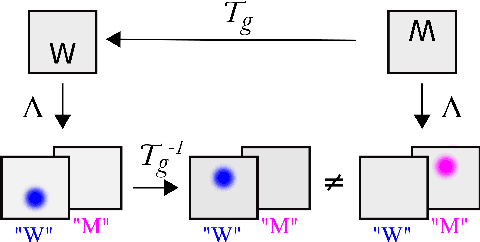
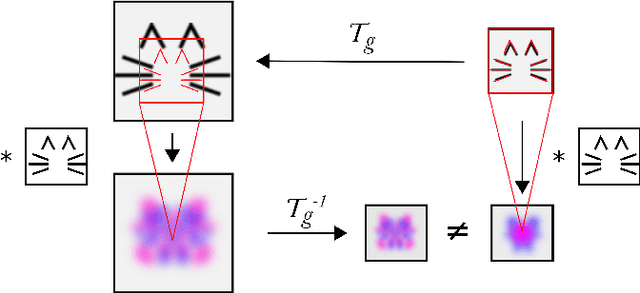
A large number of deep learning architectures use spatial transformations of CNN feature maps or filters to better deal with variability in object appearance caused by natural image transformations. In this paper, we prove that spatial transformations of CNN feature maps cannot align the feature maps of a transformed image to match those of its original, for general affine transformations, unless the extracted features are themselves invariant. Our proof is based on elementary analysis for both the single- and multi-layer network case. The results imply that methods based on spatial transformations of CNN feature maps or filters cannot replace image alignment of the input and cannot enable invariant recognition for general affine transformations, specifically not for scaling transformations or shear transformations. For rotations and reflections, spatially transforming feature maps or filters can enable invariance but only for networks with learnt or hardcoded rotation- or reflection-invariant features