Dynamics of stochastic gradient descent for two-layer neural networks in the teacher-student setup

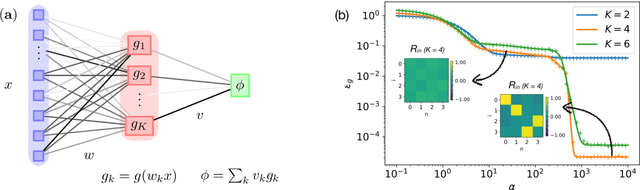
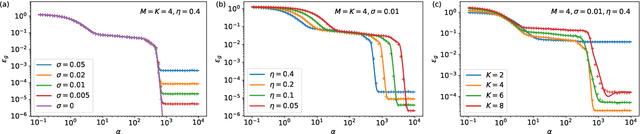
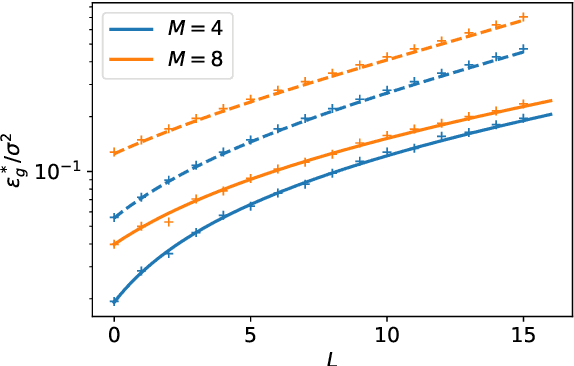
Deep neural networks achieve stellar generalisation even when they have enough parameters to easily fit all their training data. We study the dynamics and the performance of two-layer neural networks in the teacher-student setup, where one network, the student, is trained on data generated by another network, called the teacher, using stochastic gradient descent (SGD). We show how the dynamics of SGD is captured by a set of differential equations and prove that this description is asymptotically exact in the limit of large inputs. Using this framework, we calculate the final generalisation error of student networks that have more parameters than their teachers. We find that the final generalisation error of the student increases with network size when training only the first layer, but stays constant or even decreases with size when training both layers. We show that these different behaviours have their root in the different solutions SGD finds for different activation functions. Our results indicate that achieving good generalisation in neural networks goes beyond the properties of SGD alone and depends on the interplay of at least the algorithm, the model architecture, and the data set.

Generalisation dynamics of online learning in over-parameterised neural networks

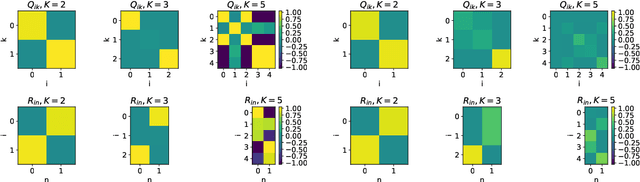
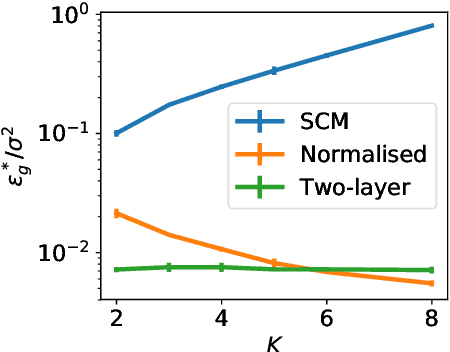
Deep neural networks achieve stellar generalisation on a variety of problems, despite often being large enough to easily fit all their training data. Here we study the generalisation dynamics of two-layer neural networks in a teacher-student setup, where one network, the student, is trained using stochastic gradient descent (SGD) on data generated by another network, called the teacher. We show how for this problem, the dynamics of SGD are captured by a set of differential equations. In particular, we demonstrate analytically that the generalisation error of the student increases linearly with the network size, with other relevant parameters held constant. Our results indicate that achieving good generalisation in neural networks depends on the interplay of at least the algorithm, its learning rate, the model architecture, and the data set.

Energy-entropy competition and the effectiveness of stochastic gradient descent in machine learning

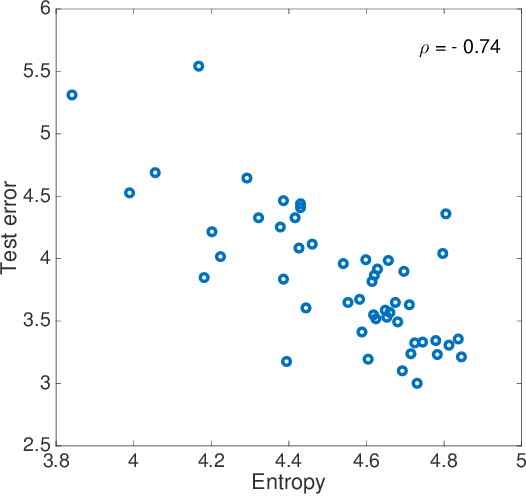
Finding parameters that minimise a loss function is at the core of many machine learning methods. The Stochastic Gradient Descent algorithm is widely used and delivers state of the art results for many problems. Nonetheless, Stochastic Gradient Descent typically cannot find the global minimum, thus its empirical effectiveness is hitherto mysterious. We derive a correspondence between parameter inference and free energy minimisation in statistical physics. The degree of undersampling plays the role of temperature. Analogous to the energy-entropy competition in statistical physics, wide but shallow minima can be optimal if the system is undersampled, as is typical in many applications. Moreover, we show that the stochasticity in the algorithm has a non-trivial correlation structure which systematically biases it towards wide minima. We illustrate our argument with two prototypical models: image classification using deep learning, and a linear neural network where we can analytically reveal the relationship between entropy and out-of-sample error.

High-dimensional dynamics of generalization error in neural networks

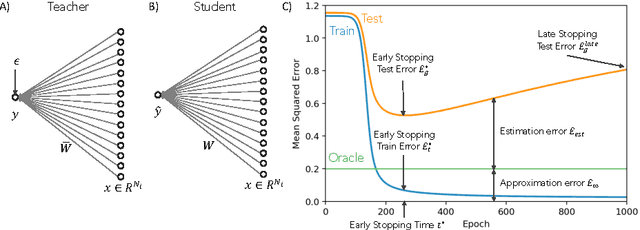
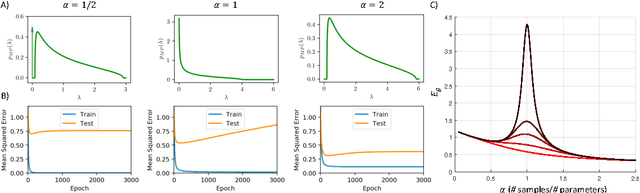
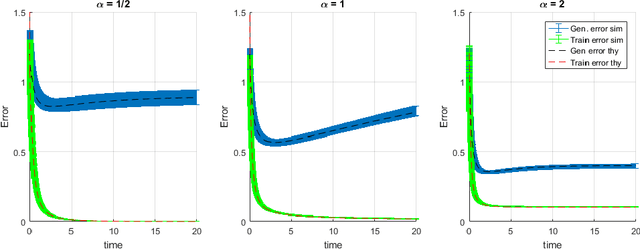
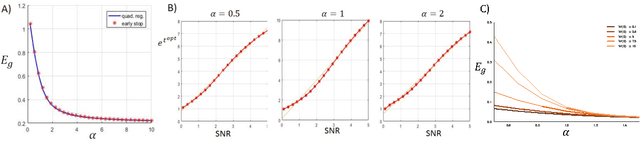
We perform an average case analysis of the generalization dynamics of large neural networks trained using gradient descent. We study the practically-relevant "high-dimensional" regime where the number of free parameters in the network is on the order of or even larger than the number of examples in the dataset. Using random matrix theory and exact solutions in linear models, we derive the generalization error and training error dynamics of learning and analyze how they depend on the dimensionality of data and signal to noise ratio of the learning problem. We find that the dynamics of gradient descent learning naturally protect against overtraining and overfitting in large networks. Overtraining is worst at intermediate network sizes, when the effective number of free parameters equals the number of samples, and thus can be reduced by making a network smaller or larger. Additionally, in the high-dimensional regime, low generalization error requires starting with small initial weights. We then turn to non-linear neural networks, and show that making networks very large does not harm their generalization performance. On the contrary, it can in fact reduce overtraining, even without early stopping or regularization of any sort. We identify two novel phenomena underlying this behavior in overcomplete models: first, there is a frozen subspace of the weights in which no learning occurs under gradient descent; and second, the statistical properties of the high-dimensional regime yield better-conditioned input correlations which protect against overtraining. We demonstrate that naive application of worst-case theories such as Rademacher complexity are inaccurate in predicting the generalization performance of deep neural networks, and derive an alternative bound which incorporates the frozen subspace and conditioning effects and qualitatively matches the behavior observed in simulation.