Generalisation dynamics of online learning in over-parameterised neural networks
Paper and Code
Jan 25, 2019
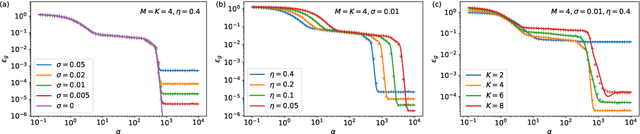
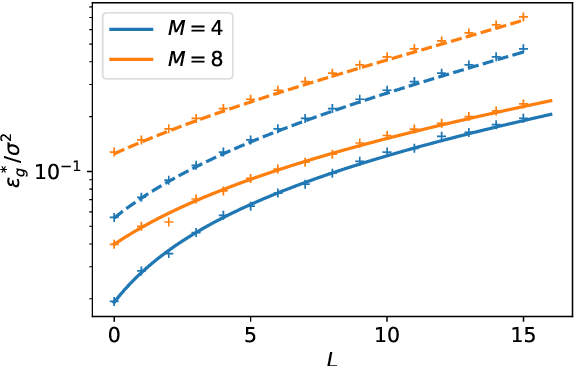
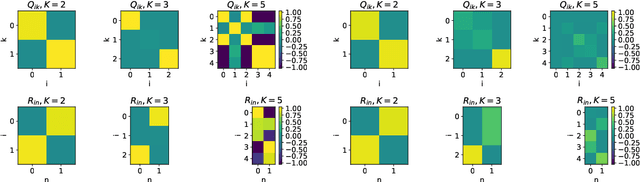
Deep neural networks achieve stellar generalisation on a variety of problems, despite often being large enough to easily fit all their training data. Here we study the generalisation dynamics of two-layer neural networks in a teacher-student setup, where one network, the student, is trained using stochastic gradient descent (SGD) on data generated by another network, called the teacher. We show how for this problem, the dynamics of SGD are captured by a set of differential equations. In particular, we demonstrate analytically that the generalisation error of the student increases linearly with the network size, with other relevant parameters held constant. Our results indicate that achieving good generalisation in neural networks depends on the interplay of at least the algorithm, its learning rate, the model architecture, and the data set.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge