Enhancing Hyper-To-Real Space Projections Through Euclidean Norm Meta-Heuristic Optimization

The continuous computational power growth in the last decades has made solving several optimization problems significant to humankind a tractable task; however, tackling some of them remains a challenge due to the overwhelming amount of candidate solutions to be evaluated, even by using sophisticated algorithms. In such a context, a set of nature-inspired stochastic methods, called meta-heuristic optimization, can provide robust approximate solutions to different kinds of problems with a small computational burden, such as derivative-free real function optimization. Nevertheless, these methods may converge to inadequate solutions if the function landscape is too harsh, e.g., enclosing too many local optima. Previous works addressed this issue by employing a hypercomplex representation of the search space, like quaternions, where the landscape becomes smoother and supposedly easier to optimize. Under this approach, meta-heuristic computations happen in the hypercomplex space, whereas variables are mapped back to the real domain before function evaluation. Despite this latter operation being performed by the Euclidean norm, we have found that after the optimization procedure has finished, it is usually possible to obtain even better solutions by employing the Minkowski $p$-norm instead and fine-tuning $p$ through an auxiliary sub-problem with neglecting additional cost and no hyperparameters. Such behavior was observed in eight well-established benchmarking functions, thus fostering a new research direction for hypercomplex meta-heuristic optimization.

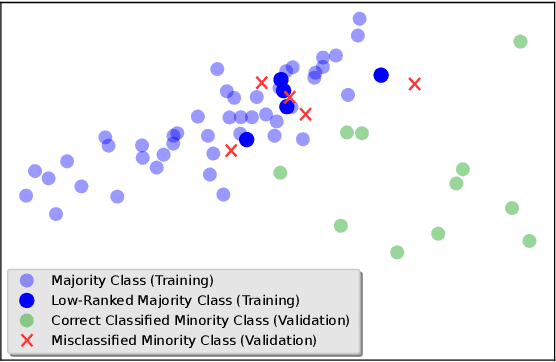
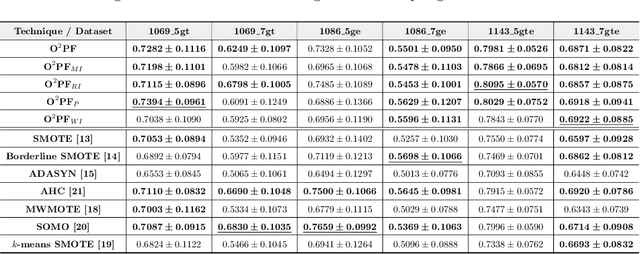
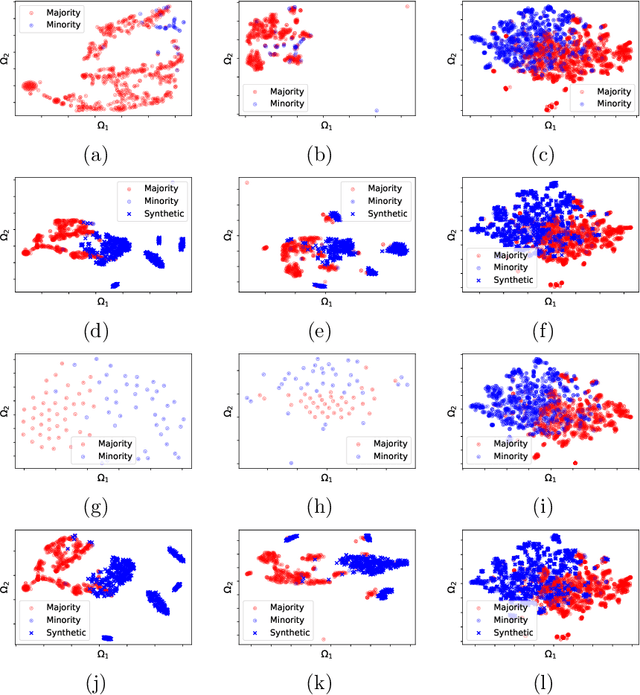
Handling Imbalanced Datasets Through Optimum-Path Forest

In the last decade, machine learning-based approaches became capable of performing a wide range of complex tasks sometimes better than humans, demanding a fraction of the time. Such an advance is partially due to the exponential growth in the amount of data available, which makes it possible to extract trustworthy real-world information from them. However, such data is generally imbalanced since some phenomena are more likely than others. Such a behavior yields considerable influence on the machine learning model's performance since it becomes biased on the more frequent data it receives. Despite the considerable amount of machine learning methods, a graph-based approach has attracted considerable notoriety due to the outstanding performance over many applications, i.e., the Optimum-Path Forest (OPF). In this paper, we propose three OPF-based strategies to deal with the imbalance problem: the $\text{O}^2$PF and the OPF-US, which are novel approaches for oversampling and undersampling, respectively, as well as a hybrid strategy combining both approaches. The paper also introduces a set of variants concerning the strategies mentioned above. Results compared against several state-of-the-art techniques over public and private datasets confirm the robustness of the proposed approaches.

$\text{O}^2$PF: Oversampling via Optimum-Path Forest for Breast Cancer Detection

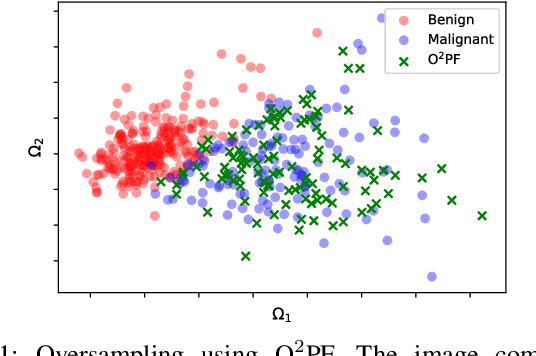
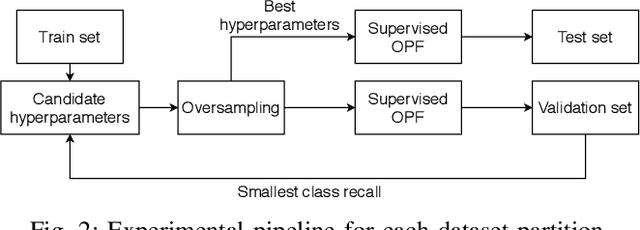
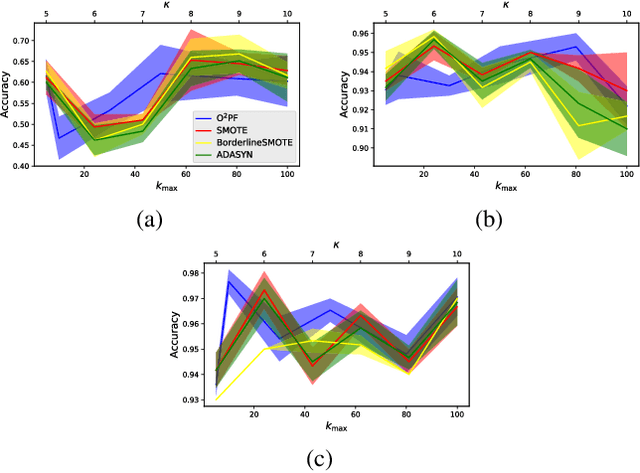
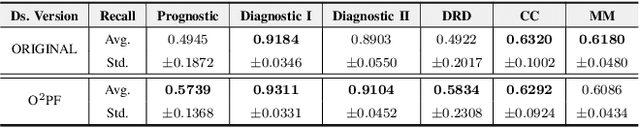
Breast cancer is among the most deadly diseases, distressing mostly women worldwide. Although traditional methods for detection have presented themselves as valid for the task, they still commonly present low accuracies and demand considerable time and effort from professionals. Therefore, a computer-aided diagnosis (CAD) system capable of providing early detection becomes hugely desirable. In the last decade, machine learning-based techniques have been of paramount importance in this context, since they are capable of extracting essential information from data and reasoning about it. However, such approaches still suffer from imbalanced data, specifically on medical issues, where the number of healthy people samples is, in general, considerably higher than the number of patients. Therefore this paper proposes the $\text{O}^2$PF, a data oversampling method based on the unsupervised Optimum-Path Forest Algorithm. Experiments conducted over the full oversampling scenario state the robustness of the model, which is compared against three well-established oversampling methods considering three breast cancer and three general-purpose tasks for medical issues datasets.