Optimising network interactions through device agnostic models

Physically implemented neural networks hold the potential to achieve the performance of deep learning models by exploiting the innate physical properties of devices as computational tools. This exploration of physical processes for computation requires to also consider their intrinsic dynamics, which can serve as valuable resources to process information. However, existing computational methods are unable to extend the success of deep learning techniques to parameters influencing device dynamics, which often lack a precise mathematical description. In this work, we formulate a universal framework to optimise interactions with dynamic physical systems in a fully data-driven fashion. The framework adopts neural stochastic differential equations as differentiable digital twins, effectively capturing both deterministic and stochastic behaviours of devices. Employing differentiation through the trained models provides the essential mathematical estimates for optimizing a physical neural network, harnessing the intrinsic temporal computation abilities of its physical nodes. To accurately model real devices' behaviours, we formulated neural-SDE variants that can operate under a variety of experimental settings. Our work demonstrates the framework's applicability through simulations and physical implementations of interacting dynamic devices, while highlighting the importance of accurately capturing system stochasticity for the successful deployment of a physically defined neural network.

A perspective on physical reservoir computing with nanomagnetic devices

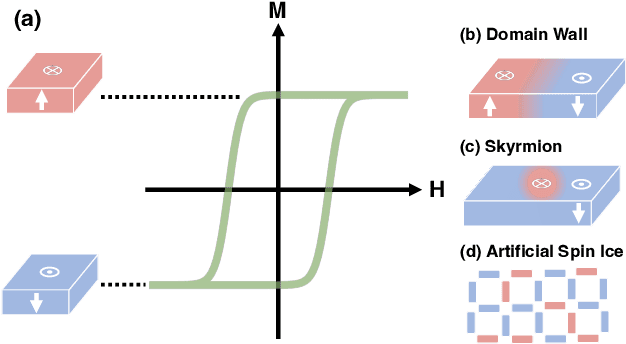
Neural networks have revolutionized the area of artificial intelligence and introduced transformative applications to almost every scientific field and industry. However, this success comes at a great price; the energy requirements for training advanced models are unsustainable. One promising way to address this pressing issue is by developing low-energy neuromorphic hardware that directly supports the algorithm's requirements. The intrinsic non-volatility, non-linearity, and memory of spintronic devices make them appealing candidates for neuromorphic devices. Here we focus on the reservoir computing paradigm, a recurrent network with a simple training algorithm suitable for computation with spintronic devices since they can provide the properties of non-linearity and memory. We review technologies and methods for developing neuromorphic spintronic devices and conclude with critical open issues to address before such devices become widely used.

EchoVPR: Echo State Networks for Visual Place Recognition

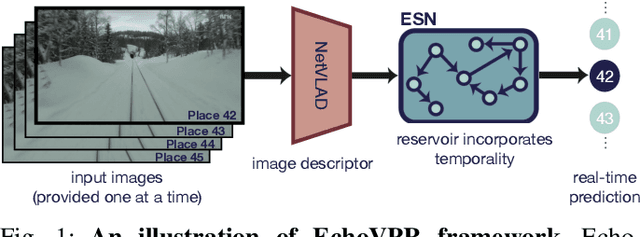
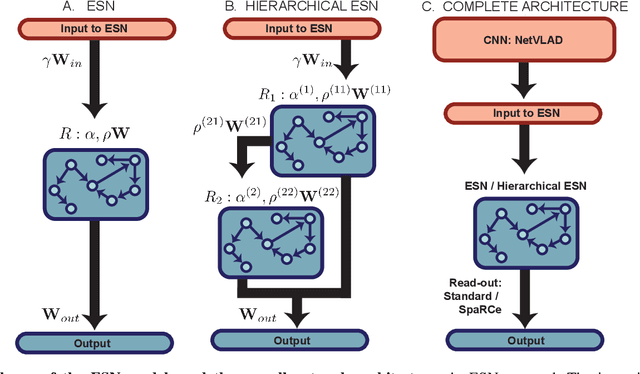
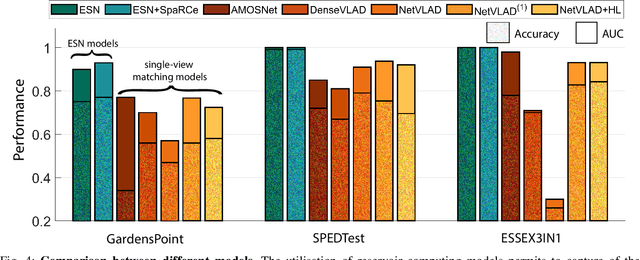
Recognising previously visited locations is an important, but unsolved, task in autonomous navigation. Current visual place recognition (VPR) benchmarks typically challenge models to recover the position of a query image (or images) from sequential datasets that include both spatial and temporal components. Recently, Echo State Network (ESN) varieties have proven particularly powerful at solving machine learning tasks that require spatio-temporal modelling. These networks are simple, yet powerful neural architectures that -- exhibiting memory over multiple time-scales and non-linear high-dimensional representations -- can discover temporal relations in the data while still maintaining linearity in the learning. In this paper, we present a series of ESNs and analyse their applicability to the VPR problem. We report that the addition of ESNs to pre-processed convolutional neural networks led to a dramatic boost in performance in comparison to non-recurrent networks in four standard benchmarks (GardensPoint, SPEDTest, ESSEX3IN1, Nordland) demonstrating that ESNs are able to capture the temporal structure inherent in VPR problems. Moreover, we show that ESNs can outperform class-leading VPR models which also exploit the sequential dynamics of the data. Finally, our results demonstrate that ESNs also improve generalisation abilities, robustness, and accuracy further supporting their suitability to VPR applications.

Exploiting Multiple Timescales in Hierarchical Echo State Networks

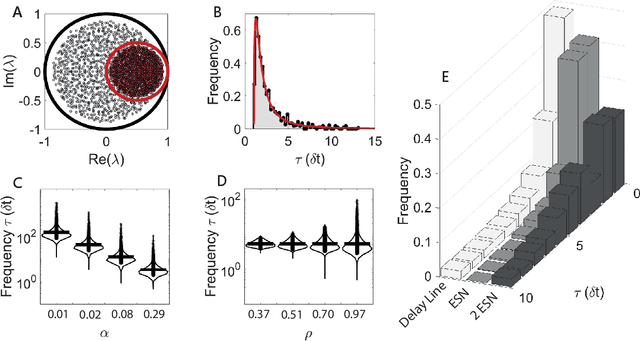
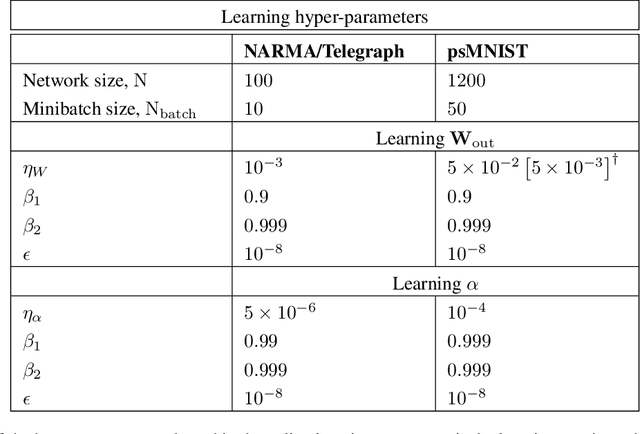
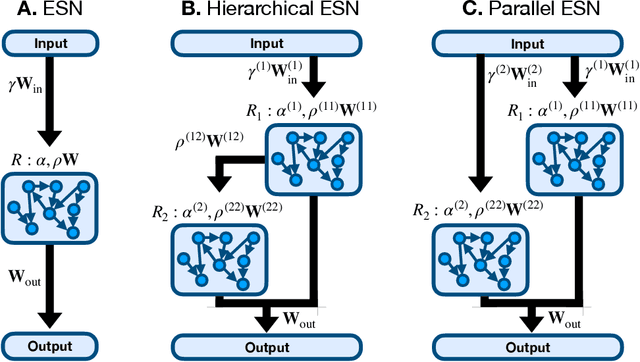
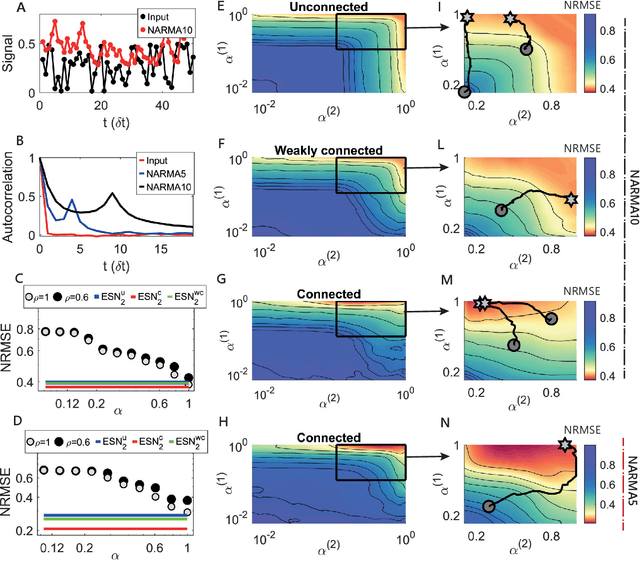
Echo state networks (ESNs) are a powerful form of reservoir computing that only require training of linear output weights whilst the internal reservoir is formed of fixed randomly connected neurons. With a correctly scaled connectivity matrix, the neurons' activity exhibits the echo-state property and responds to the input dynamics with certain timescales. Tuning the timescales of the network can be necessary for treating certain tasks, and some environments require multiple timescales for an efficient representation. Here we explore the timescales in hierarchical ESNs, where the reservoir is partitioned into two smaller linked reservoirs with distinct properties. Over three different tasks (NARMA10, a reconstruction task in a volatile environment, and psMNIST), we show that by selecting the hyper-parameters of each partition such that they focus on different timescales, we achieve a significant performance improvement over a single ESN. Through a linear analysis, and under the assumption that the timescales of the first partition are much shorter than the second's (typically corresponding to optimal operating conditions), we interpret the feedforward coupling of the partitions in terms of an effective representation of the input signal, provided by the first partition to the second, whereby the instantaneous input signal is expanded into a weighted combination of its time derivatives. Furthermore, we propose a data-driven approach to optimise the hyper-parameters through a gradient descent optimisation method that is an online approximation of backpropagation through time. We demonstrate the application of the online learning rule across all the tasks considered.

SpaRCe: Sparse reservoir computing

"Sparse" neural networks, in which relatively few neurons or connections are active, are common in both machine learning and neuroscience. Whereas in machine learning, "sparseness" is related to a penalty term which effectively leads to some connecting weights becoming small or zero, in biological brains, sparseness is often created when high spiking thresholds prevent neuronal activity. Inspired by neuroscience, here we introduce sparseness into a reservoir computing network via neuron-specific learnable thresholds of activity, allowing neurons with low thresholds to give output but silencing outputs from neurons with high thresholds. This approach, which we term "SpaRCe", optimises the sparseness level of the reservoir and applies the threshold mechanism to the information received by the read-out weights. Both the read-out weights and the thresholds are learned by a standard on-line gradient rule that minimises an error function on the outputs of the network. Threshold learning occurs by the balance of two opposing forces: reducing inter-neuronal correlations in the reservoir by deactivating redundant neurons, while increasing the activity of neurons participating in correct decisions. We test SpaRCe in a set of classification problems and find that introducing threshold learning improves performance compared to standard reservoir computing networks.

Learning sparsity in reservoir computing through a novel bio-inspired algorithm

The mushroom body is the key network for the representation of learned olfactory stimuli in Drosophila and insects. The sparse activity of Kenyon cells, the principal neurons in the mushroom body, plays a key role in the learned classification of different odours. In the specific case of the fruit fly, the sparseness of the network is enforced by an inhibitory feedback neuron called APL, and by an intrinsic high firing threshold of the Kenyon cells. In this work we took inspiration from the fruit fly brain to formulate a novel machine learning algorithm that is able to optimize the sparsity level of a reservoir by changing the firing thresholds of the nodes. The sparsity is only applied on the readout layer so as not to change the timescales of the reservoir and to allow the derivation of a one-layer update rule for the firing thresholds. The proposed algorithm is a combination of learning a neuron-specific sparsity threshold via gradient descent and a global sparsity threshold via a Markov chain Monte Carlo method. The proposed model outperforms the standard gradient descent, which is limited to the readout weights of the reservoir, on two example tasks. It demonstrates how the learnt sparse representation can lead to better classification performance, memorization ability and convergence time.