Machine learning using magnetic stochastic synapses

The impressive performance of artificial neural networks has come at the cost of high energy usage and CO$_2$ emissions. Unconventional computing architectures, with magnetic systems as a candidate, have potential as alternative energy-efficient hardware, but, still face challenges, such as stochastic behaviour, in implementation. Here, we present a methodology for exploiting the traditionally detrimental stochastic effects in magnetic domain-wall motion in nanowires. We demonstrate functional binary stochastic synapses alongside a gradient learning rule that allows their training with applicability to a range of stochastic systems. The rule, utilising the mean and variance of the neuronal output distribution, finds a trade-off between synaptic stochasticity and energy efficiency depending on the number of measurements of each synapse. For single measurements, the rule results in binary synapses with minimal stochasticity, sacrificing potential performance for robustness. For multiple measurements, synaptic distributions are broad, approximating better-performing continuous synapses. This observation allows us to choose design principles depending on the desired performance and the device's operational speed and energy cost. We verify performance on physical hardware, showing it is comparable to a standard neural network.

Exploiting Multiple Timescales in Hierarchical Echo State Networks

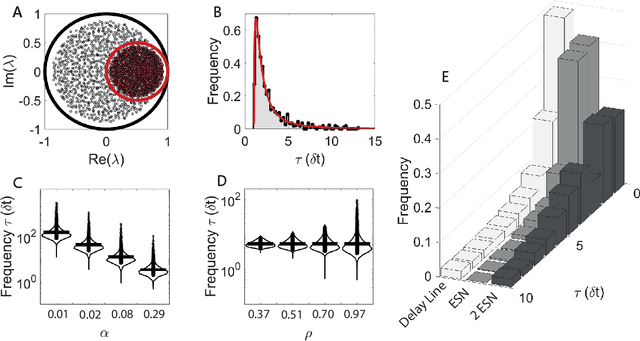
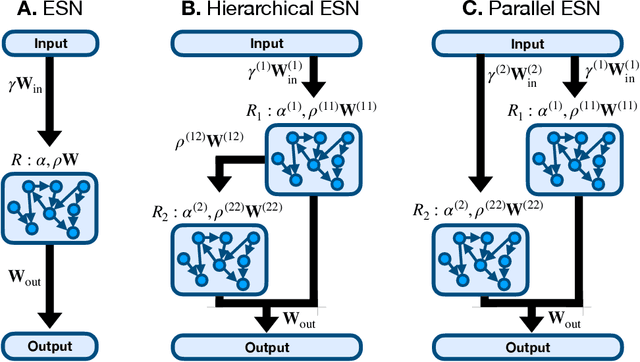
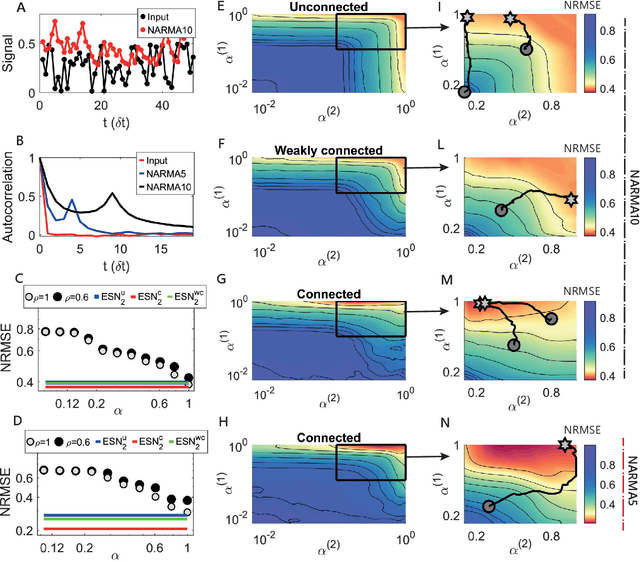
Echo state networks (ESNs) are a powerful form of reservoir computing that only require training of linear output weights whilst the internal reservoir is formed of fixed randomly connected neurons. With a correctly scaled connectivity matrix, the neurons' activity exhibits the echo-state property and responds to the input dynamics with certain timescales. Tuning the timescales of the network can be necessary for treating certain tasks, and some environments require multiple timescales for an efficient representation. Here we explore the timescales in hierarchical ESNs, where the reservoir is partitioned into two smaller linked reservoirs with distinct properties. Over three different tasks (NARMA10, a reconstruction task in a volatile environment, and psMNIST), we show that by selecting the hyper-parameters of each partition such that they focus on different timescales, we achieve a significant performance improvement over a single ESN. Through a linear analysis, and under the assumption that the timescales of the first partition are much shorter than the second's (typically corresponding to optimal operating conditions), we interpret the feedforward coupling of the partitions in terms of an effective representation of the input signal, provided by the first partition to the second, whereby the instantaneous input signal is expanded into a weighted combination of its time derivatives. Furthermore, we propose a data-driven approach to optimise the hyper-parameters through a gradient descent optimisation method that is an online approximation of backpropagation through time. We demonstrate the application of the online learning rule across all the tasks considered.