Visibility Optimization for Surveillance-Evasion Games

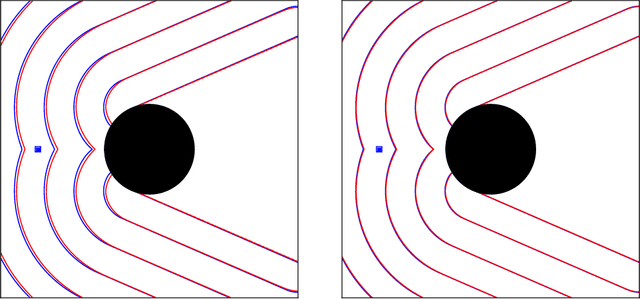
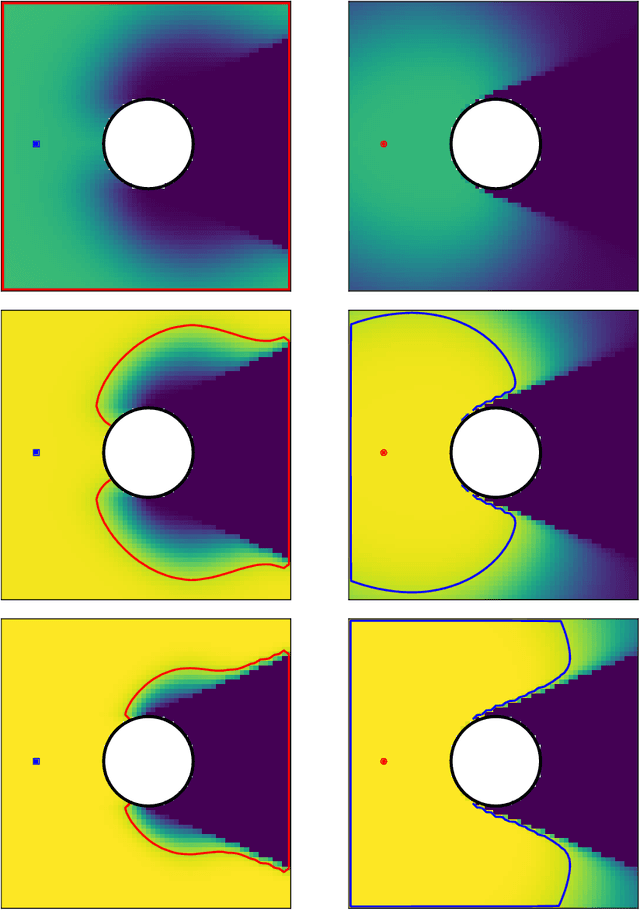
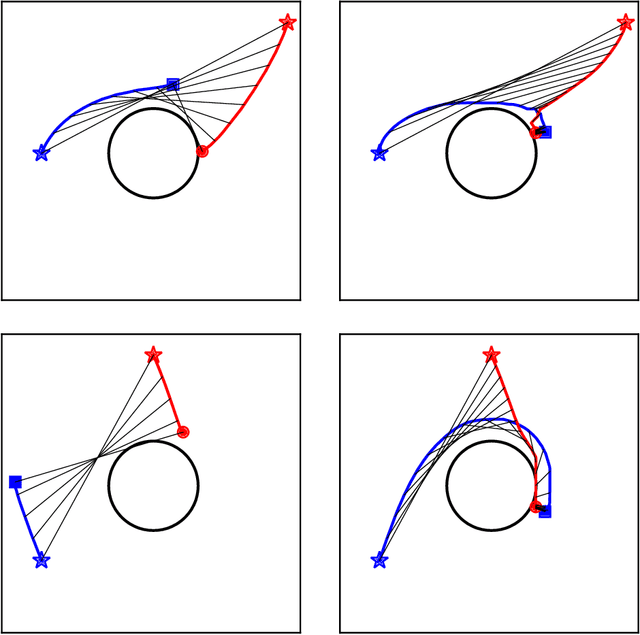
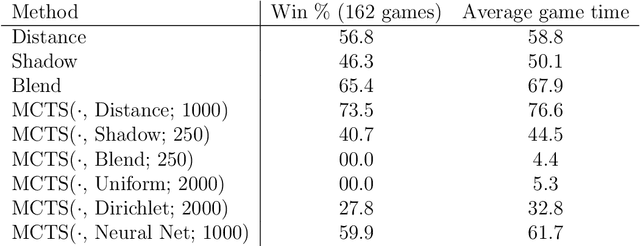
We consider surveillance-evasion differential games, where a pursuer must try to constantly maintain visibility of a moving evader. The pursuer loses as soon as the evader becomes occluded. Optimal controls for game can be formulated as a Hamilton-Jacobi-Isaac equation. We use an upwind scheme to compute the feedback value function, corresponding to the end-game time of the differential game. Although the value function enables optimal controls, it is prohibitively expensive to compute, even for a single pursuer and single evader on a small grid. We consider a discrete variant of the surveillance-game. We propose two locally optimal strategies based on the static value function for the surveillance-evasion game with multiple pursuers and evaders. We show that Monte Carlo tree search and self-play reinforcement learning can train a deep neural network to generate reasonable strategies for on-line game play. Given enough computational resources and offline training time, the proposed model can continue to improve its policies and efficiently scale to higher resolutions.

Nearest Neighbor Sampling of Point Sets using Random Rays

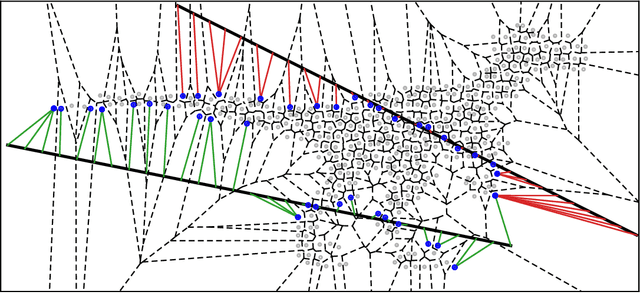
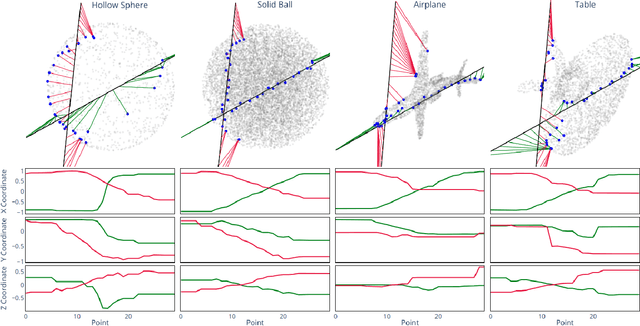
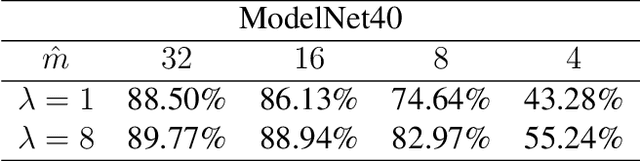
We propose a new framework for the sampling, compression, and analysis of distributions of point sets and other geometric objects embedded in Euclidean spaces. A set of randomly selected rays are projected onto their closest points in the data set, forming the ray signature. From the signature, statistical information about the data set, as well as certain geometrical information, can be extracted, independent of the ray set. We present promising results from "RayNN", a neural network for the classification of point clouds based on ray signatures.

Strategy Synthesis for Surveillance-Evasion Games with Learning-Enabled Visibility Optimization

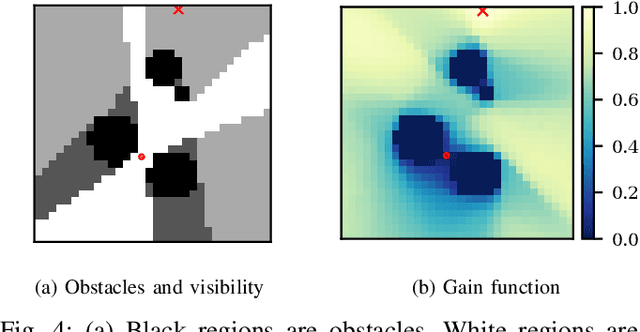
This paper studies a two-player game with a quantitative surveillance requirement on an adversarial target moving in a discrete state space and a secondary objective to maximize short-term visibility of the environment. We impose the surveillance requirement as a temporal logic constraint.We then use a greedy approach to determine vantage points that optimize a notion of information gain, namely, the number of newly-seen states. By using a convolutional neural network trained on a class of environments, we can efficiently approximate the information gain at each potential vantage point.Subsequent vantage points are chosen such that moving to that location will not jeopardize the surveillance requirement, regardless of any future action chosen by the target. Our method combines guarantees of correctness from formal methods with the scalability of machine learning to provide an efficient approach for surveillance-constrained visibility optimization.

Autonomous Exploration, Reconstruction, and Surveillance of 3D Environments Aided by Deep Learning

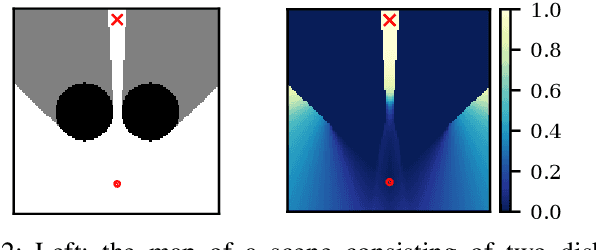
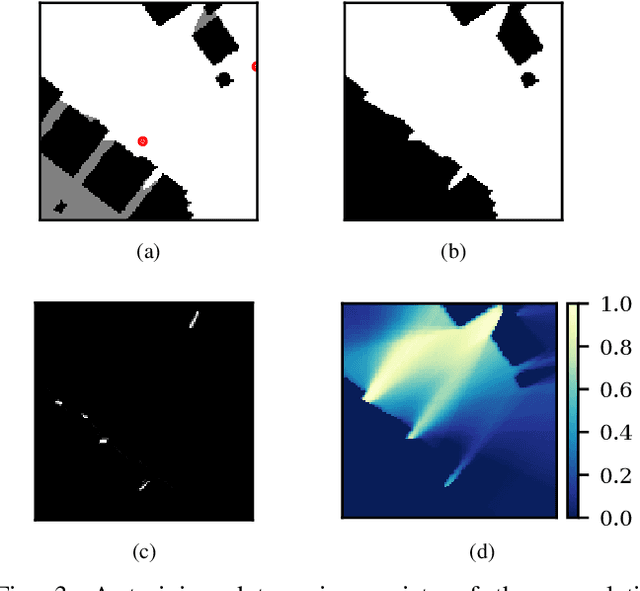
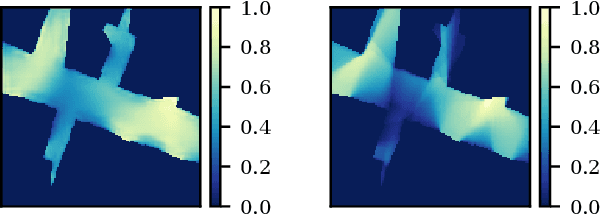
We study the problem of visibility-based exploration, reconstruction and surveillance in the context of supervised learning. Using a level set representation of data and information, we train a convolutional neural network to determine vantage points that maximize visibility. We show that this method drastically reduces the on-line computational cost and determines a small set of vantage points that solve the problem. This enables us to efficiently produce highly-resolved and topologically accurate maps of complex 3D environments. We present realistic simulations on 2D and 3D urban environments.