Efficient Numerical Wave Propagation Enhanced By An End-to-End Deep Learning Model

Recent advances in wave modeling use sufficiently accurate fine solver outputs to train a neural network that enhances the accuracy of a fast but inaccurate coarse solver. In this paper we build upon the work of Nguyen and Tsai (2023) and present a novel unified system that integrates a numerical solver with a deep learning component into an end-to-end framework. In the proposed setting, we investigate refinements to the network architecture and data generation algorithm. A stable and fast solver further allows the use of Parareal, a parallel-in-time algorithm to correct high-frequency wave components. Our results show that the cohesive structure improves performance without sacrificing speed, and demonstrate the importance of temporal dynamics, as well as Parareal, for accurate wave propagation.

Linear Regression on Manifold Structured Data: the Impact of Extrinsic Geometry on Solutions

In this paper, we study linear regression applied to data structured on a manifold. We assume that the data manifold is smooth and is embedded in a Euclidean space, and our objective is to reveal the impact of the data manifold's extrinsic geometry on the regression. Specifically, we analyze the impact of the manifold's curvatures (or higher order nonlinearity in the parameterization when the curvatures are locally zero) on the uniqueness of the regression solution. Our findings suggest that the corresponding linear regression does not have a unique solution when the embedded submanifold is flat in some dimensions. Otherwise, the manifold's curvature (or higher order nonlinearity in the embedding) may contribute significantly, particularly in the solution associated with the normal directions of the manifold. Our findings thus reveal the role of data manifold geometry in ensuring the stability of regression models for out-of-distribution inferences.

Side-effects of Learning from Low Dimensional Data Embedded in an Euclidean Space

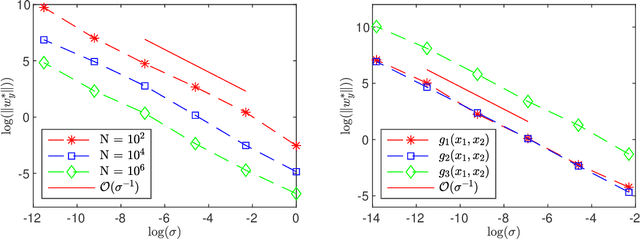
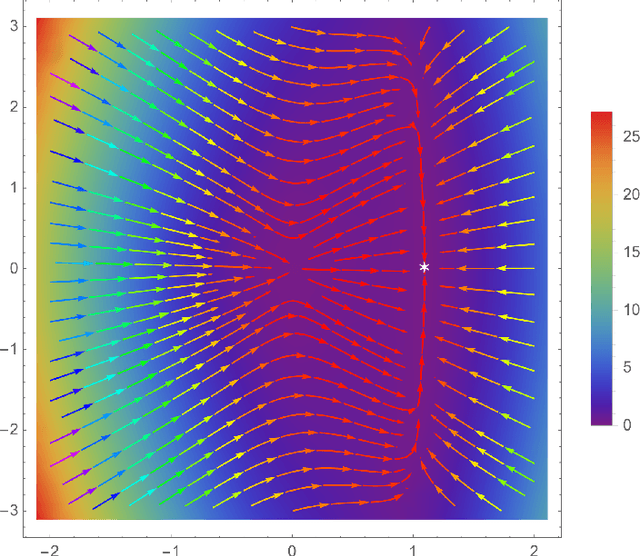
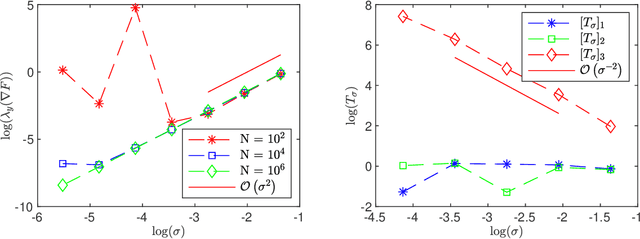
The low dimensional manifold hypothesis posits that the data found in many applications, such as those involving natural images, lie (approximately) on low dimensional manifolds embedded in a high dimensional Euclidean space. In this setting, a typical neural network defines a function that takes a finite number of vectors in the embedding space as input. However, one often needs to consider evaluating the optimized network at points outside the training distribution. This paper considers the case in which the training data is distributed in a linear subspace of $\mathbb R^d$. We derive estimates on the variation of the learning function, defined by a neural network, in the direction transversal to the subspace. We study the potential regularization effects associated with the network's depth and noise in the codimension of the data manifold. We also present additional side effects in training due to the presence of noise.

Strategy Synthesis for Surveillance-Evasion Games with Learning-Enabled Visibility Optimization

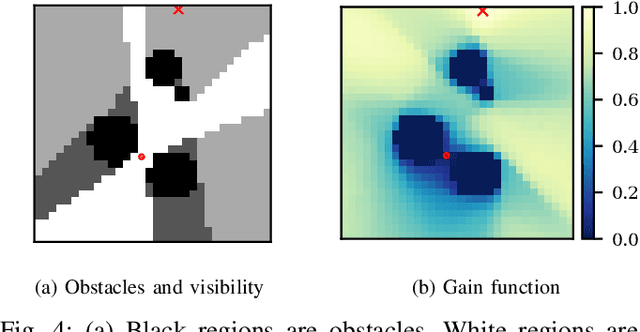
This paper studies a two-player game with a quantitative surveillance requirement on an adversarial target moving in a discrete state space and a secondary objective to maximize short-term visibility of the environment. We impose the surveillance requirement as a temporal logic constraint.We then use a greedy approach to determine vantage points that optimize a notion of information gain, namely, the number of newly-seen states. By using a convolutional neural network trained on a class of environments, we can efficiently approximate the information gain at each potential vantage point.Subsequent vantage points are chosen such that moving to that location will not jeopardize the surveillance requirement, regardless of any future action chosen by the target. Our method combines guarantees of correctness from formal methods with the scalability of machine learning to provide an efficient approach for surveillance-constrained visibility optimization.

An Elastic Image Registration Approach for Wireless Capsule Endoscope Localization

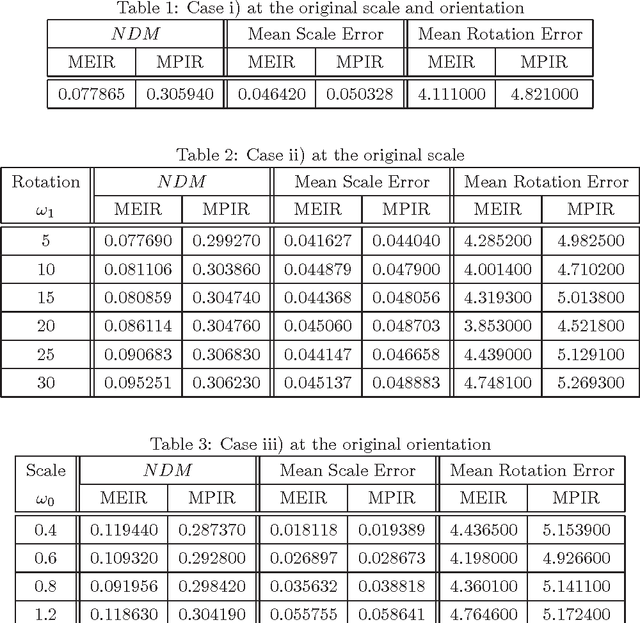
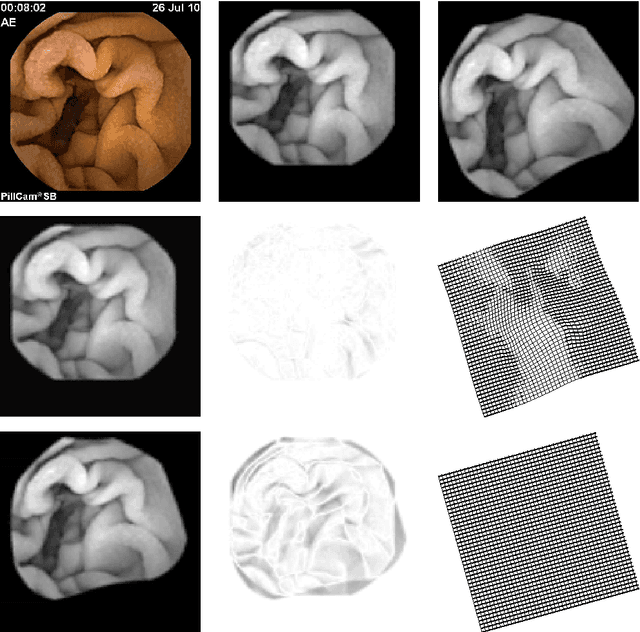
Wireless Capsule Endoscope (WCE) is an innovative imaging device that permits physicians to examine all the areas of the Gastrointestinal (GI) tract. It is especially important for the small intestine, where traditional invasive endoscopies cannot reach. Although WCE represents an extremely important advance in medical imaging, a major drawback that remains unsolved is the WCE precise location in the human body during its operating time. This is mainly due to the complex physiological environment and the inherent capsule effects during its movement. When an abnormality is detected, in the WCE images, medical doctors do not know precisely where this abnormality is located relative to the intestine and therefore they can not proceed efficiently with the appropriate therapy. The primary objective of the present paper is to give a contribution to WCE localization, using image-based methods. The main focus of this work is on the description of a multiscale elastic image registration approach, its experimental application on WCE videos, and comparison with a multiscale affine registration. The proposed approach includes registrations that capture both rigid-like and non-rigid deformations, due respectively to the rigid-like WCE movement and the elastic deformation of the small intestine originated by the GI peristaltic movement. Under this approach a qualitative information about the WCE speed can be obtained, as well as the WCE location and orientation via projective geometry. The results of the experimental tests with real WCE video frames show the good performance of the proposed approach, when elastic deformations of the small intestine are involved in successive frames, and its superiority with respect to a multiscale affine image registration, which accounts for rigid-like deformations only and discards elastic deformations.