Visibility Optimization for Surveillance-Evasion Games
Paper and Code
Oct 18, 2020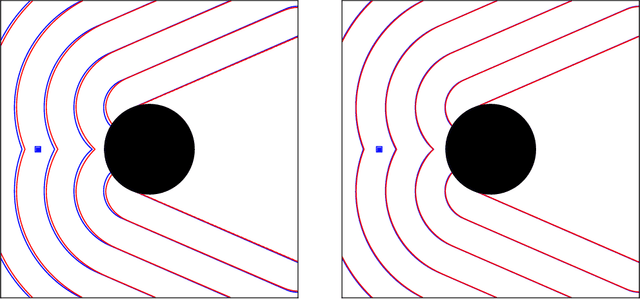
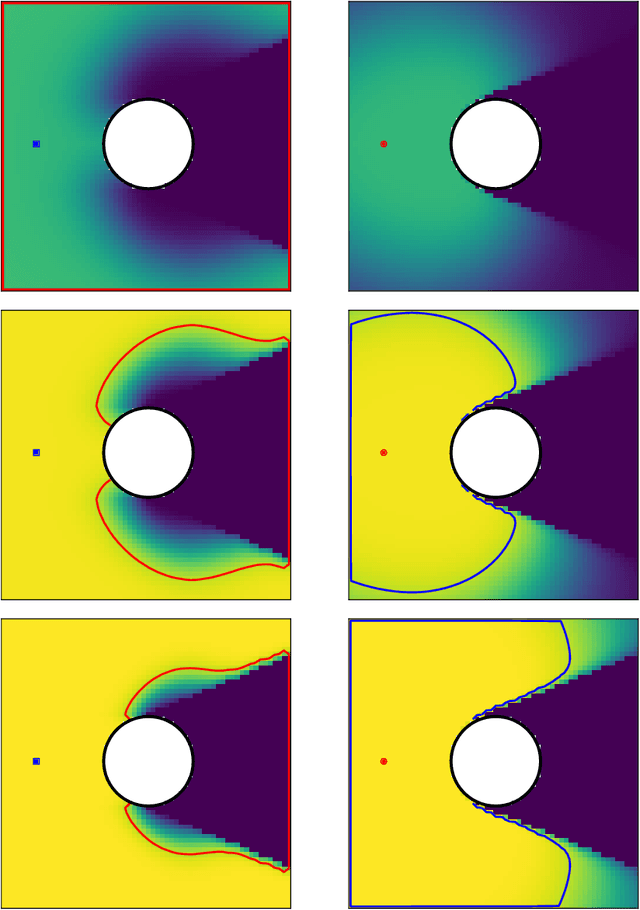
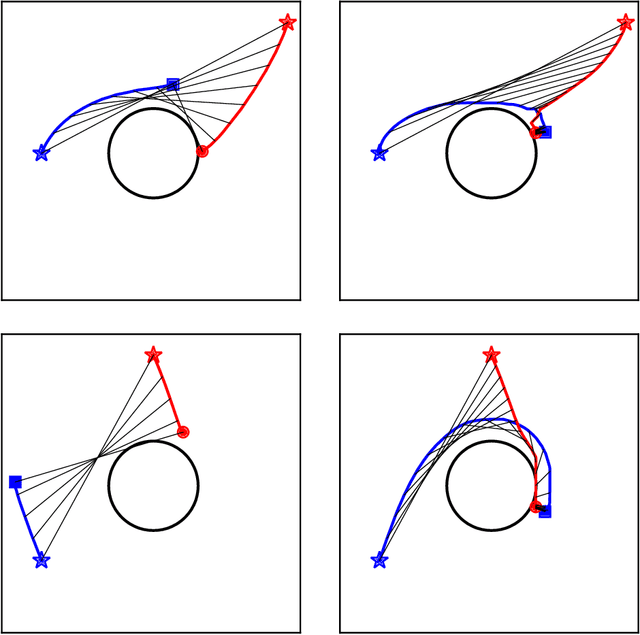
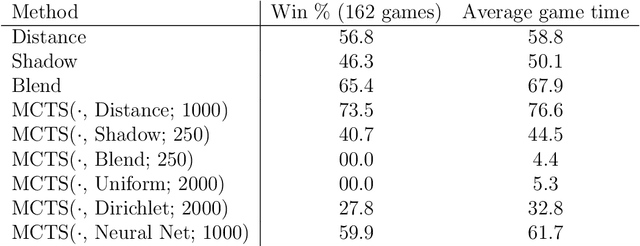
We consider surveillance-evasion differential games, where a pursuer must try to constantly maintain visibility of a moving evader. The pursuer loses as soon as the evader becomes occluded. Optimal controls for game can be formulated as a Hamilton-Jacobi-Isaac equation. We use an upwind scheme to compute the feedback value function, corresponding to the end-game time of the differential game. Although the value function enables optimal controls, it is prohibitively expensive to compute, even for a single pursuer and single evader on a small grid. We consider a discrete variant of the surveillance-game. We propose two locally optimal strategies based on the static value function for the surveillance-evasion game with multiple pursuers and evaders. We show that Monte Carlo tree search and self-play reinforcement learning can train a deep neural network to generate reasonable strategies for on-line game play. Given enough computational resources and offline training time, the proposed model can continue to improve its policies and efficiently scale to higher resolutions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge