Vision-Language Pseudo-Labels for Single-Positive Multi-Label Learning

This paper presents a novel approach to Single-Positive Multi-label Learning. In general multi-label learning, a model learns to predict multiple labels or categories for a single input image. This is in contrast with standard multi-class image classification, where the task is predicting a single label from many possible labels for an image. Single-Positive Multi-label Learning (SPML) specifically considers learning to predict multiple labels when there is only a single annotation per image in the training data. Multi-label learning is in many ways a more realistic task than single-label learning as real-world data often involves instances belonging to multiple categories simultaneously; however, most common computer vision datasets predominantly contain single labels due to the inherent complexity and cost of collecting multiple high quality annotations for each instance. We propose a novel approach called Vision-Language Pseudo-Labeling (VLPL), which uses a vision-language model to suggest strong positive and negative pseudo-labels, and outperforms the current SOTA methods by 5.5% on Pascal VOC, 18.4% on MS-COCO, 15.2% on NUS-WIDE, and 8.4% on CUB-Birds. Our code and data are available at https://github.com/mvrl/VLPL.

Lie Group Auto-Encoder

In this paper, we propose an auto-encoder based generative neural network model whose encoder compresses the inputs into vectors in the tangent space of a special Lie group manifold: upper triangular positive definite affine transform matrices (UTDATs). UTDATs are representations of Gaussian distributions and can straightforwardly generate Gaussian distributed samples. Therefore, the encoder is trained together with a decoder (generator) which takes Gaussian distributed latent vectors as input. Compared with related generative models such as variational auto-encoder, the proposed model incorporates the information on geometric properties of Gaussian distributions. As a special case, we derive an exponential mapping layer for diagonal Gaussian UTDATs which eliminates matrix exponential operator compared with general exponential mapping in Lie group theory. Moreover, we derive an intrinsic loss for UTDAT Lie group which can be calculated as l-2 loss in the tangent space. Furthermore, inspired by the Lie group theory, we propose to use the Lie algebra vectors rather than the raw parameters (e.g. mean) of Gaussian distributions as compressed representations of original inputs. Experimental results verity the effectiveness of the proposed new generative model and the benefits gained from the Lie group structural information of UTDATs.

Adaptive Edge Features Guided Graph Attention Networks

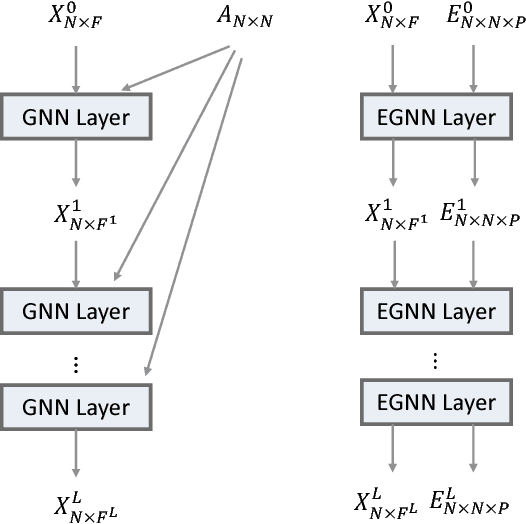
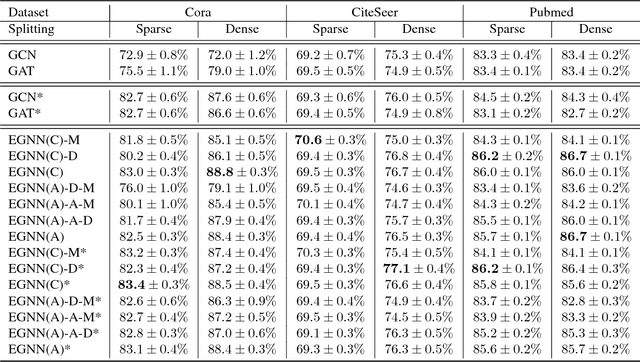
Edge features contain important information about graphs. However, current state-of-the-art neural network models designed for graph learning do not consider incorporating edge features, especially multi-dimensional edge features. In this paper, we propose an attention mechanism which combines both node features and edge features. Guided by the edge features, the attention mechanism on a pair of graph nodes will not only depend on node contents, but also ajust automatically with respect to the properties of the edge connecting these two nodes. Moreover, the edge features are adjusted by the attention function and fed to the next layer, which means our edge features are adaptive across network layers. As a result, our proposed adaptive edge features guided graph attention model can consolidate a rich source of graph information that current state-of-the-art graph learning methods cannot. We apply our proposed model to graph node classification, and experimental results on three citaion network datasets and a biological network dataset show that out method outperforms the current state-of-the-art methods, testifying to the discriminative capability of edge features and the effectiveness of our adaptive edge features guided attention model. Additional ablation experimental study further shows that both the edge features and adaptiveness components contribute to our model.

Lie Algebrized Gaussians for Image Representation

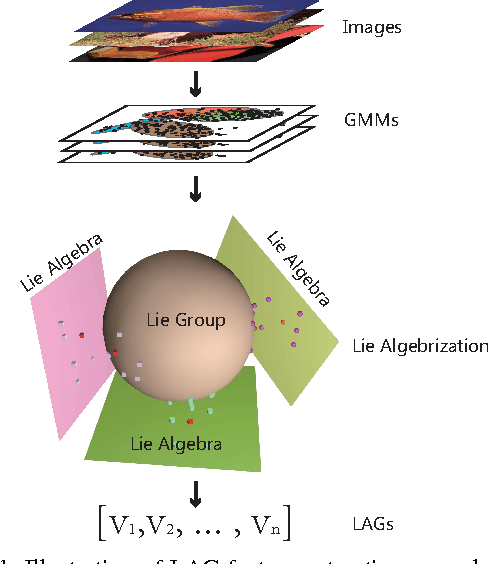
We present an image representation method which is derived from analyzing Gaussian probability density function (\emph{pdf}) space using Lie group theory. In our proposed method, images are modeled by Gaussian mixture models (GMMs) which are adapted from a globally trained GMM called universal background model (UBM). Then we vectorize the GMMs based on two facts: (1) components of image-specific GMMs are closely grouped together around their corresponding component of the UBM due to the characteristic of the UBM adaption procedure; (2) Gaussian \emph{pdf}s form a Lie group, which is a differentiable manifold rather than a vector space. We map each Gaussian component to the tangent vector space (named Lie algebra) of Lie group at the manifold position of UBM. The final feature vector, named Lie algebrized Gaussians (LAG) is then constructed by combining the Lie algebrized Gaussian components with mixture weights. We apply LAG features to scene category recognition problem and observe state-of-the-art performance on 15Scenes benchmark.