Lie Algebrized Gaussians for Image Representation
Paper and Code
May 09, 2017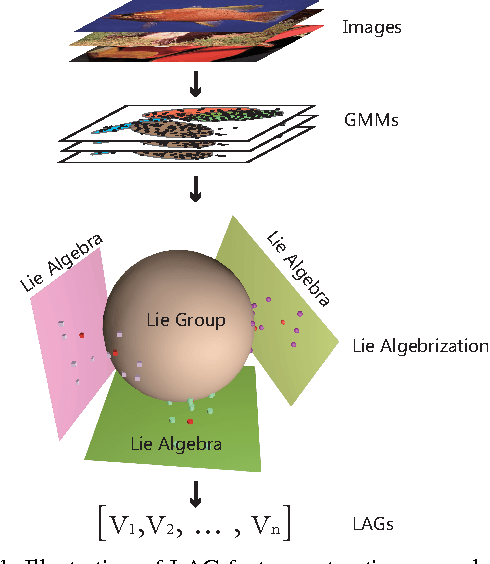


We present an image representation method which is derived from analyzing Gaussian probability density function (\emph{pdf}) space using Lie group theory. In our proposed method, images are modeled by Gaussian mixture models (GMMs) which are adapted from a globally trained GMM called universal background model (UBM). Then we vectorize the GMMs based on two facts: (1) components of image-specific GMMs are closely grouped together around their corresponding component of the UBM due to the characteristic of the UBM adaption procedure; (2) Gaussian \emph{pdf}s form a Lie group, which is a differentiable manifold rather than a vector space. We map each Gaussian component to the tangent vector space (named Lie algebra) of Lie group at the manifold position of UBM. The final feature vector, named Lie algebrized Gaussians (LAG) is then constructed by combining the Lie algebrized Gaussian components with mixture weights. We apply LAG features to scene category recognition problem and observe state-of-the-art performance on 15Scenes benchmark.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge