Conditional Density Estimation with Histogram Trees

Conditional density estimation (CDE) goes beyond regression by modeling the full conditional distribution, providing a richer understanding of the data than just the conditional mean in regression. This makes CDE particularly useful in critical application domains. However, interpretable CDE methods are understudied. Current methods typically employ kernel-based approaches, using kernel functions directly for kernel density estimation or as basis functions in linear models. In contrast, despite their conceptual simplicity and visualization suitability, tree-based methods -- which are arguably more comprehensible -- have been largely overlooked for CDE tasks. Thus, we propose the Conditional Density Tree (CDTree), a fully non-parametric model consisting of a decision tree in which each leaf is formed by a histogram model. Specifically, we formalize the problem of learning a CDTree using the minimum description length (MDL) principle, which eliminates the need for tuning the hyperparameter for regularization. Next, we propose an iterative algorithm that, although greedily, searches the optimal histogram for every possible node split. Our experiments demonstrate that, in comparison to existing interpretable CDE methods, CDTrees are both more accurate (as measured by the log-loss) and more robust against irrelevant features. Further, our approach leads to smaller tree sizes than existing tree-based models, which benefits interpretability.

Probabilistic Truly Unordered Rule Sets

Rule set learning has recently been frequently revisited because of its interpretability. Existing methods have several shortcomings though. First, most existing methods impose orders among rules, either explicitly or implicitly, which makes the models less comprehensible. Second, due to the difficulty of handling conflicts caused by overlaps (i.e., instances covered by multiple rules), existing methods often do not consider probabilistic rules. Third, learning classification rules for multi-class target is understudied, as most existing methods focus on binary classification or multi-class classification via the ``one-versus-rest" approach. To address these shortcomings, we propose TURS, for Truly Unordered Rule Sets. To resolve conflicts caused by overlapping rules, we propose a novel model that exploits the probabilistic properties of our rule sets, with the intuition of only allowing rules to overlap if they have similar probabilistic outputs. We next formalize the problem of learning a TURS model based on the MDL principle and develop a carefully designed heuristic algorithm. We benchmark against a wide range of rule-based methods and demonstrate that our method learns rule sets that have lower model complexity and highly competitive predictive performance. In addition, we empirically show that rules in our model are empirically ``independent" and hence truly unordered.

Truly Unordered Probabilistic Rule Sets for Multi-class Classification

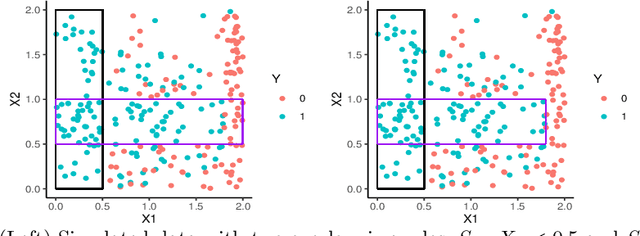
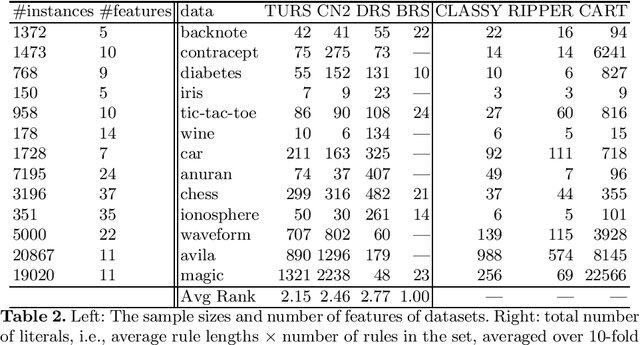
Rule set learning has long been studied and has recently been frequently revisited due to the need for interpretable models. Still, existing methods have several shortcomings: 1) most recent methods require a binary feature matrix as input, learning rules directly from numeric variables is understudied; 2) existing methods impose orders among rules, either explicitly or implicitly, which harms interpretability; and 3) currently no method exists for learning probabilistic rule sets for multi-class target variables (there is only a method for probabilistic rule lists). We propose TURS, for Truly Unordered Rule Sets, which addresses these shortcomings. We first formalise the problem of learning truly unordered rule sets. To resolve conflicts caused by overlapping rules, i.e., instances covered by multiple rules, we propose a novel approach that exploits the probabilistic properties of our rule sets. We next develop a two-phase heuristic algorithm that learns rule sets by carefully growing rules. An important innovation is that we use a surrogate score to take the global potential of the rule set into account when learning a local rule. Finally, we empirically demonstrate that, compared to non-probabilistic and (explicitly or implicitly) ordered state-of-the-art methods, our method learns rule sets that not only have better interpretability (i.e., they are smaller and truly unordered), but also better predictive performance.

Unsupervised Discretization by Two-dimensional MDL-based Histogram

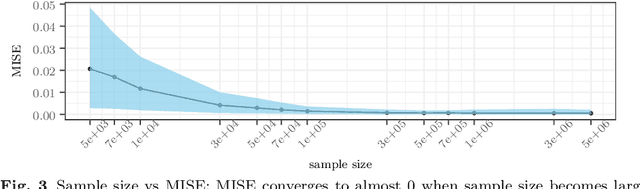
Unsupervised discretization is a crucial step in many knowledge discovery tasks. The state-of-the-art method for one-dimensional data infers locally adaptive histograms using the minimum description length (MDL) principle, but the multi-dimensional case is far less studied: current methods consider the dimensions one at a time (if not independently), which result in discretizations based on rectangular cells of adaptive size. Unfortunately, this approach is unable to adequately characterize dependencies among dimensions and/or results in discretizations consisting of more cells (or bins) than is desirable. To address this problem, we propose an expressive model class that allows for far more flexible partitions of two-dimensional data. We extend the state of the art for the one-dimensional case to obtain a model selection problem based on the normalised maximum likelihood, a form of refined MDL. As the flexibility of our model class comes at the cost of a vast search space, we introduce a heuristic algorithm, named PALM, which partitions each dimension alternately and then merges neighbouring regions, all using the MDL principle. Experiments on synthetic data show that PALM 1) accurately reveals ground truth partitions that are within the model class (i.e., the search space), given a large enough sample size; 2) approximates well a wide range of partitions outside the model class; 3) converges, in contrast to its closest competitor IPD; and 4) is self-adaptive with regard to both sample size and local density structure of the data despite being parameter-free. Finally, we apply our algorithm to two geographic datasets to demonstrate its real-world potential.