Unsupervised Discretization by Two-dimensional MDL-based Histogram

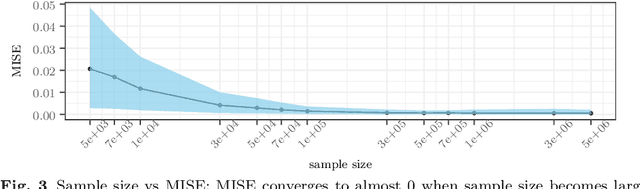
Unsupervised discretization is a crucial step in many knowledge discovery tasks. The state-of-the-art method for one-dimensional data infers locally adaptive histograms using the minimum description length (MDL) principle, but the multi-dimensional case is far less studied: current methods consider the dimensions one at a time (if not independently), which result in discretizations based on rectangular cells of adaptive size. Unfortunately, this approach is unable to adequately characterize dependencies among dimensions and/or results in discretizations consisting of more cells (or bins) than is desirable. To address this problem, we propose an expressive model class that allows for far more flexible partitions of two-dimensional data. We extend the state of the art for the one-dimensional case to obtain a model selection problem based on the normalised maximum likelihood, a form of refined MDL. As the flexibility of our model class comes at the cost of a vast search space, we introduce a heuristic algorithm, named PALM, which partitions each dimension alternately and then merges neighbouring regions, all using the MDL principle. Experiments on synthetic data show that PALM 1) accurately reveals ground truth partitions that are within the model class (i.e., the search space), given a large enough sample size; 2) approximates well a wide range of partitions outside the model class; 3) converges, in contrast to its closest competitor IPD; and 4) is self-adaptive with regard to both sample size and local density structure of the data despite being parameter-free. Finally, we apply our algorithm to two geographic datasets to demonstrate its real-world potential.