Calibrated Multivariate Regression with Application to Neural Semantic Basis Discovery

We propose a calibrated multivariate regression method named CMR for fitting high dimensional multivariate regression models. Compared with existing methods, CMR calibrates regularization for each regression task with respect to its noise level so that it simultaneously attains improved finite-sample performance and tuning insensitiveness. Theoretically, we provide sufficient conditions under which CMR achieves the optimal rate of convergence in parameter estimation. Computationally, we propose an efficient smoothed proximal gradient algorithm with a worst-case numerical rate of convergence $\cO(1/\epsilon)$, where $\epsilon$ is a pre-specified accuracy of the objective function value. We conduct thorough numerical simulations to illustrate that CMR consistently outperforms other high dimensional multivariate regression methods. We also apply CMR to solve a brain activity prediction problem and find that it is as competitive as a handcrafted model created by human experts. The R package \texttt{camel} implementing the proposed method is available on the Comprehensive R Archive Network \url{http://cran.r-project.org/web/packages/camel/}.

Neyman-Pearson Classification under High-Dimensional Settings

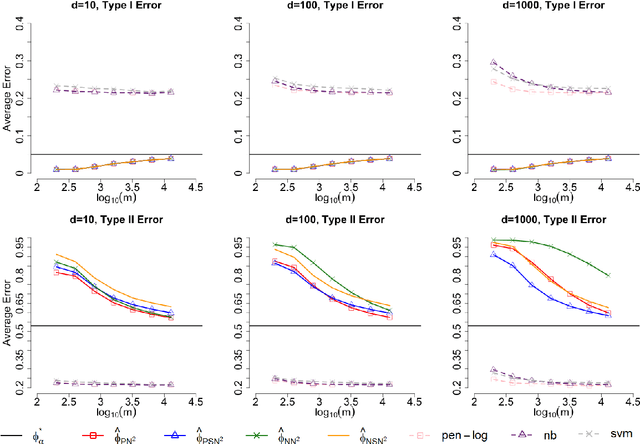
Most existing binary classification methods target on the optimization of the overall classification risk and may fail to serve some real-world applications such as cancer diagnosis, where users are more concerned with the risk of misclassifying one specific class than the other. Neyman-Pearson (NP) paradigm was introduced in this context as a novel statistical framework for handling asymmetric type I/II error priorities. It seeks classifiers with a minimal type II error and a constrained type I error under a user specified level. This article is the first attempt to construct classifiers with guaranteed theoretical performance under the NP paradigm in high-dimensional settings. Based on the fundamental Neyman-Pearson Lemma, we used a plug-in approach to construct NP-type classifiers for Naive Bayes models. The proposed classifiers satisfy the NP oracle inequalities, which are natural NP paradigm counterparts of the oracle inequalities in classical binary classification. Besides their desirable theoretical properties, we also demonstrated their numerical advantages in prioritized error control via both simulation and real data studies.

Optimization for Compressed Sensing: the Simplex Method and Kronecker Sparsification

In this paper we present two new approaches to efficiently solve large-scale compressed sensing problems. These two ideas are independent of each other and can therefore be used either separately or together. We consider all possibilities. For the first approach, we note that the zero vector can be taken as the initial basic (infeasible) solution for the linear programming problem and therefore, if the true signal is very sparse, some variants of the simplex method can be expected to take only a small number of pivots to arrive at a solution. We implemented one such variant and demonstrate a dramatic improvement in computation time on very sparse signals. The second approach requires a redesigned sensing mechanism in which the vector signal is stacked into a matrix. This allows us to exploit the Kronecker compressed sensing (KCS) mechanism. We show that the Kronecker sensing requires stronger conditions for perfect recovery compared to the original vector problem. However, the Kronecker sensing, modeled correctly, is a much sparser linear optimization problem. Hence, algorithms that benefit from sparse problem representation, such as interior-point methods, can solve the Kronecker sensing problems much faster than the corresponding vector problem. In our numerical studies, we demonstrate a ten-fold improvement in the computation time.