Classifying States of the Hopfield Network with Improved Accuracy, Generalization, and Interpretability

We extend the existing work on Hopfield network state classification, employing more complex models that remain interpretable, such as densely-connected feed-forward deep neural networks and support vector machines. The states of the Hopfield network can be grouped into several classes, including learned (those presented during training), spurious (stable states that were not learned), and prototype (stable states that were not learned but are representative for a subset of learned states). It is often useful to determine to what class a given state belongs to; for example to ignore spurious states when retrieving from the network. Previous research has approached the state classification task with simple linear methods, most notably the stability ratio. We deepen the research on classifying states from prototype-regime Hopfield networks, investigating how varying the factors strengthening prototypes influences the state classification task. We study the generalizability of different classification models when trained on states derived from different prototype tasks -- for example, can a network trained on a Hopfield network with 10 prototypes classify states from a network with 20 prototypes? We find that simple models often outperform the stability ratio while remaining interpretable. These models require surprisingly little training data and generalize exceptionally well to states generated by a range of Hopfield networks, even those that were trained on exceedingly different datasets.

Conceptual capacity and effective complexity of neural networks

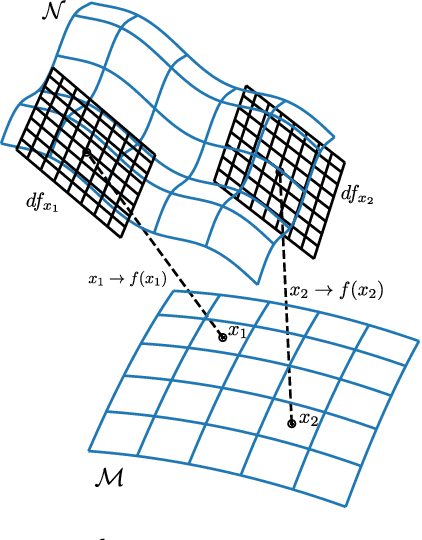
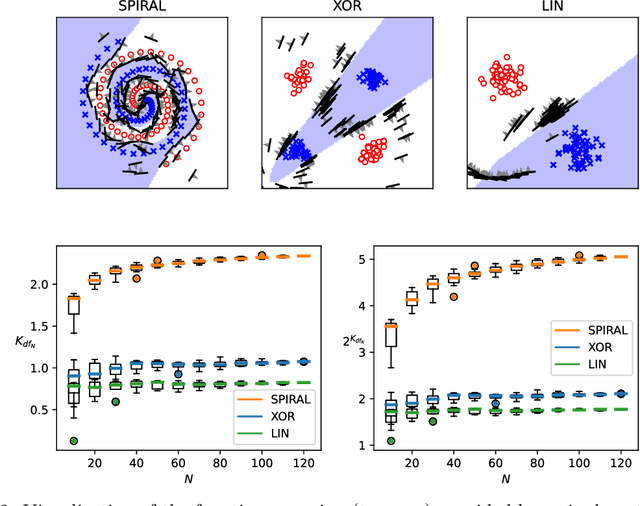
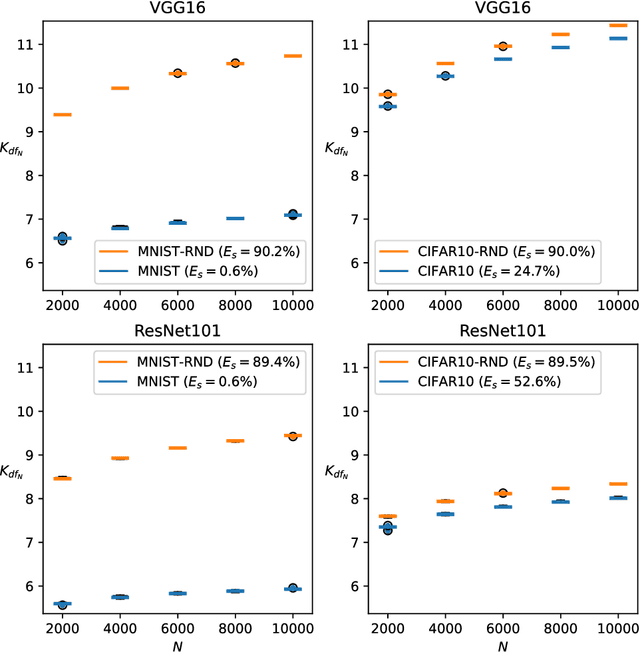
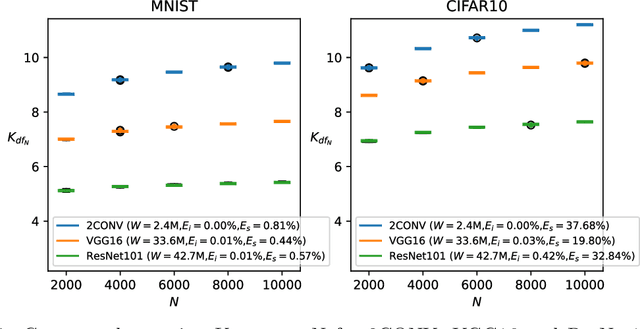
We propose a complexity measure of a neural network mapping function based on the diversity of the set of tangent spaces from different inputs. Treating each tangent space as a linear PAC concept we use an entropy-based measure of the bundle of concepts in order to estimate the conceptual capacity of the network. The theoretical maximal capacity of a ReLU network is equivalent to the number of its neurons. In practice however, due to correlations between neuron activities within the network, the actual capacity can be remarkably small, even for very big networks. Empirical evaluations show that this new measure is correlated with the complexity of the mapping function and thus the generalisation capabilities of the corresponding network. It captures the effective, as oppose to the theoretical, complexity of the network function. We also showcase some uses of the proposed measure for analysis and comparison of trained neural network models.

MIME: Mutual Information Minimisation Exploration

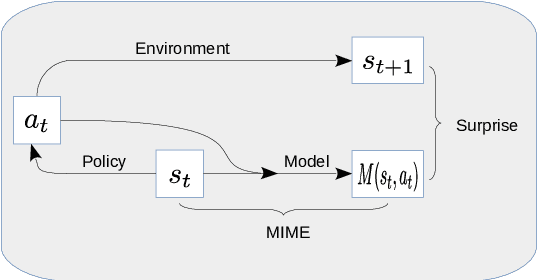
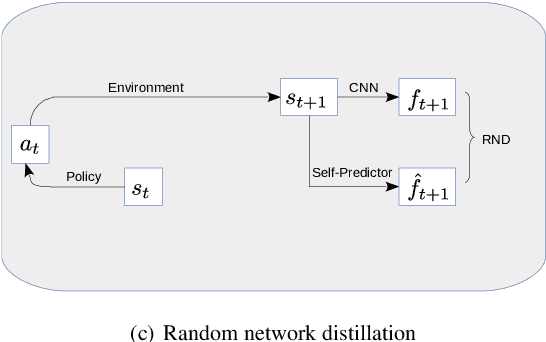
We show that reinforcement learning agents that learn by surprise (surprisal) get stuck at abrupt environmental transition boundaries because these transitions are difficult to learn. We propose a counter-intuitive solution that we call Mutual Information Minimising Exploration (MIME) where an agent learns a latent representation of the environment without trying to predict the future states. We show that our agent performs significantly better over sharp transition boundaries while matching the performance of surprisal driven agents elsewhere. In particular, we show state-of-the-art performance on difficult learning games such as Gravitar, Montezuma's Revenge and Doom.

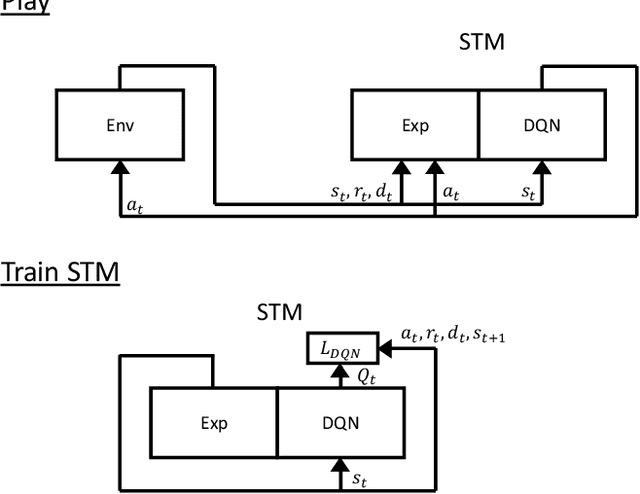
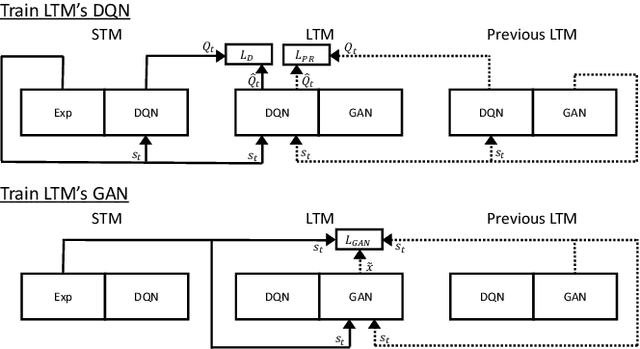
GRIm-RePR: Prioritising Generating Important Features for Pseudo-Rehearsal

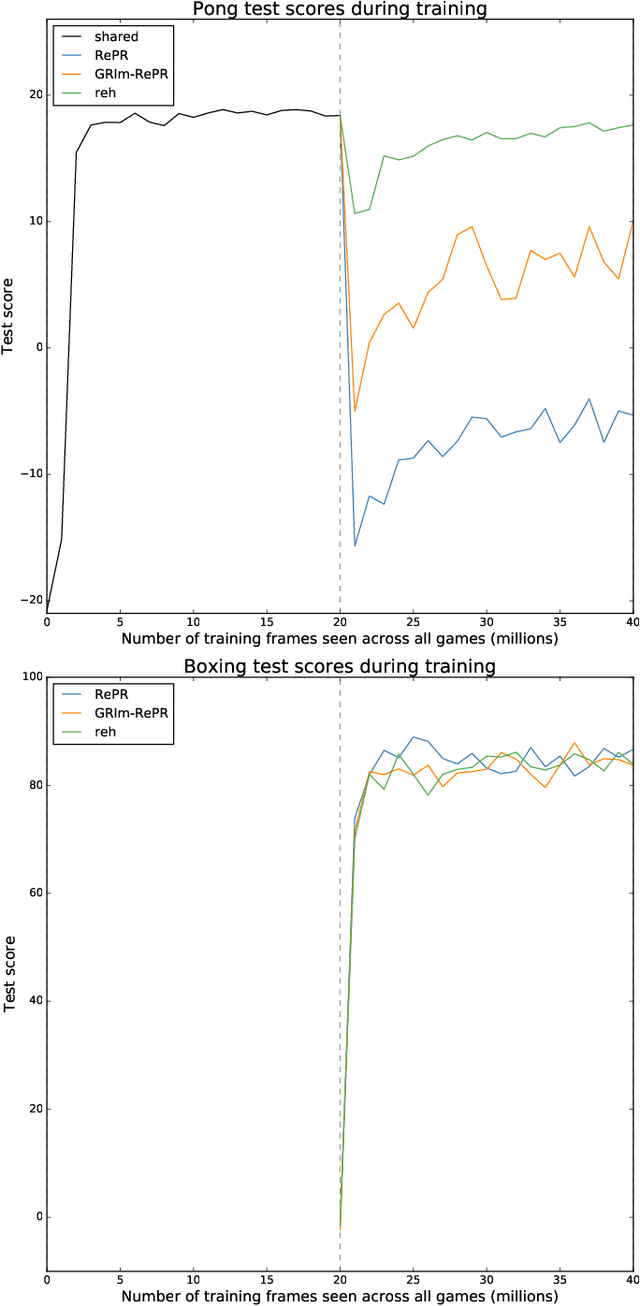
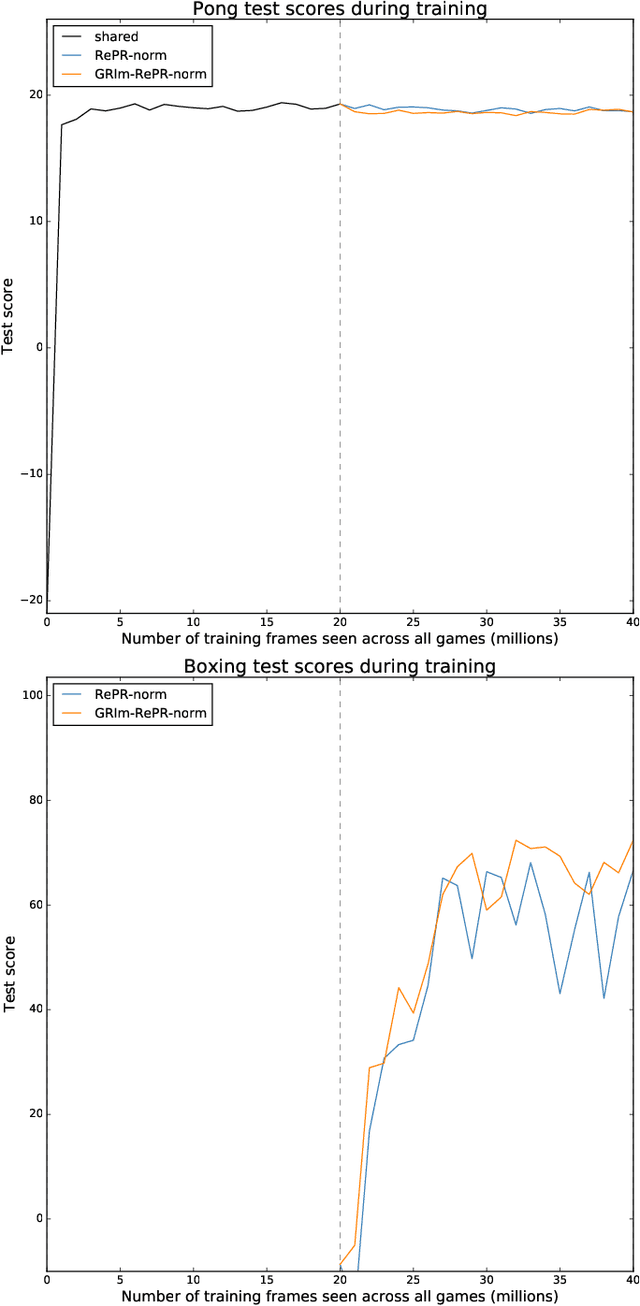
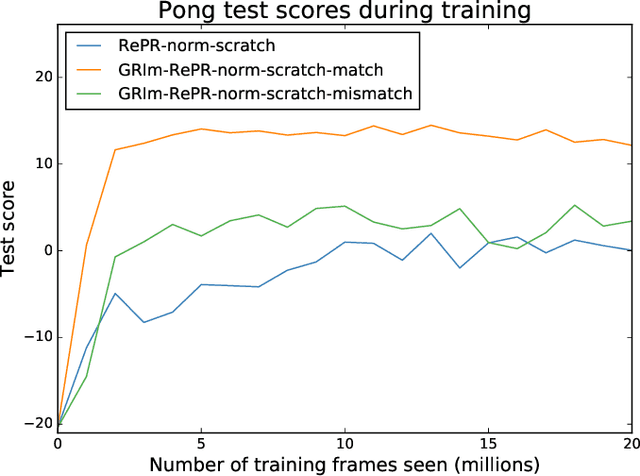
Pseudo-rehearsal allows neural networks to learn a sequence of tasks without forgetting how to perform in earlier tasks. Preventing forgetting is achieved by introducing a generative network which can produce data from previously seen tasks so that it can be rehearsed along side learning the new task. This has been found to be effective in both supervised and reinforcement learning. Our current work aims to further prevent forgetting by encouraging the generator to accurately generate features important for task retention. More specifically, the generator is improved by introducing a second discriminator into the Generative Adversarial Network which learns to classify between real and fake items from the intermediate activation patterns that they produce when fed through a continual learning agent. Using Atari 2600 games, we experimentally find that improving the generator can considerably reduce catastrophic forgetting compared to the standard pseudo-rehearsal methods used in deep reinforcement learning. Furthermore, we propose normalising the Q-values taught to the long-term system as we observe this substantially reduces catastrophic forgetting by minimising the interference between tasks' reward functions.

VASE: Variational Assorted Surprise Exploration for Reinforcement Learning

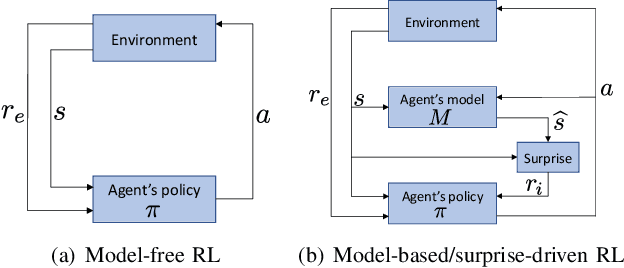
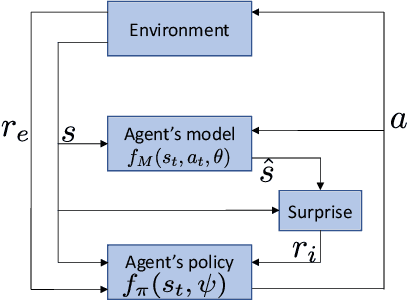
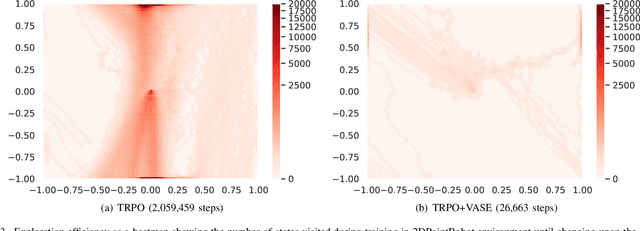
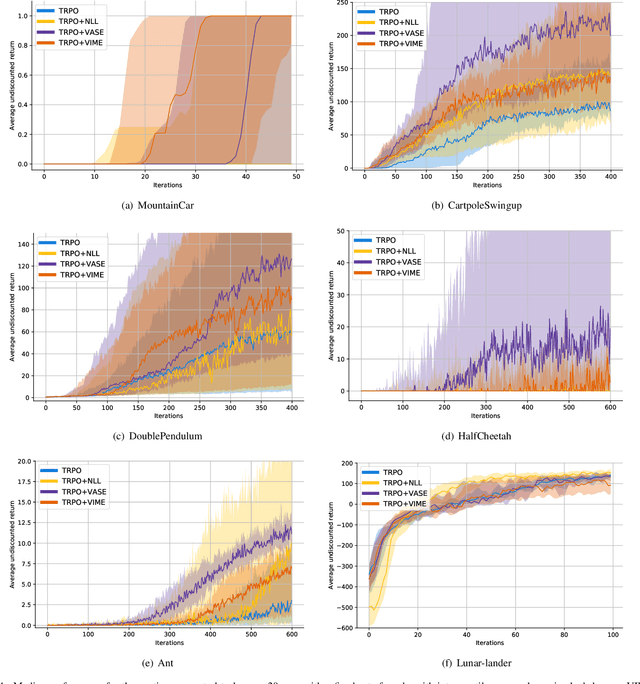
Exploration in environments with continuous control and sparse rewards remains a key challenge in reinforcement learning (RL). Recently, surprise has been used as an intrinsic reward that encourages systematic and efficient exploration. We introduce a new definition of surprise and its RL implementation named Variational Assorted Surprise Exploration (VASE). VASE uses a Bayesian neural network as a model of the environment dynamics and is trained using variational inference, alternately updating the accuracy of the agent's model and policy. Our experiments show that in continuous control sparse reward environments VASE outperforms other surprise-based exploration techniques.

Switched linear projections and inactive state sensitivity for deep neural network interpretability

We introduce switched linear projections for expressing the activity of a neuron in a ReLU-based deep neural network in terms of a single linear projection in the input space. The method works by isolating the active subnetwork, a series of linear transformations, that completely determine the entire computation of the deep network for a given input instance. We also propose that for interpretability it is more instructive and meaningful to focus on the patterns that deactive the neurons in the network, which are ignored by the exisiting methods that implicitly track only the active aspect of the network's computation. We introduce a novel interpretability method for the inactive state sensitivity (Insens). Comparison against existing methods shows that Insens is more robust (in the presence of noise), more complete (in terms of patterns that affect the computation) and a very effective interpretability method for deep neural networks.

Pseudo-Rehearsal: Achieving Deep Reinforcement Learning without Catastrophic Forgetting

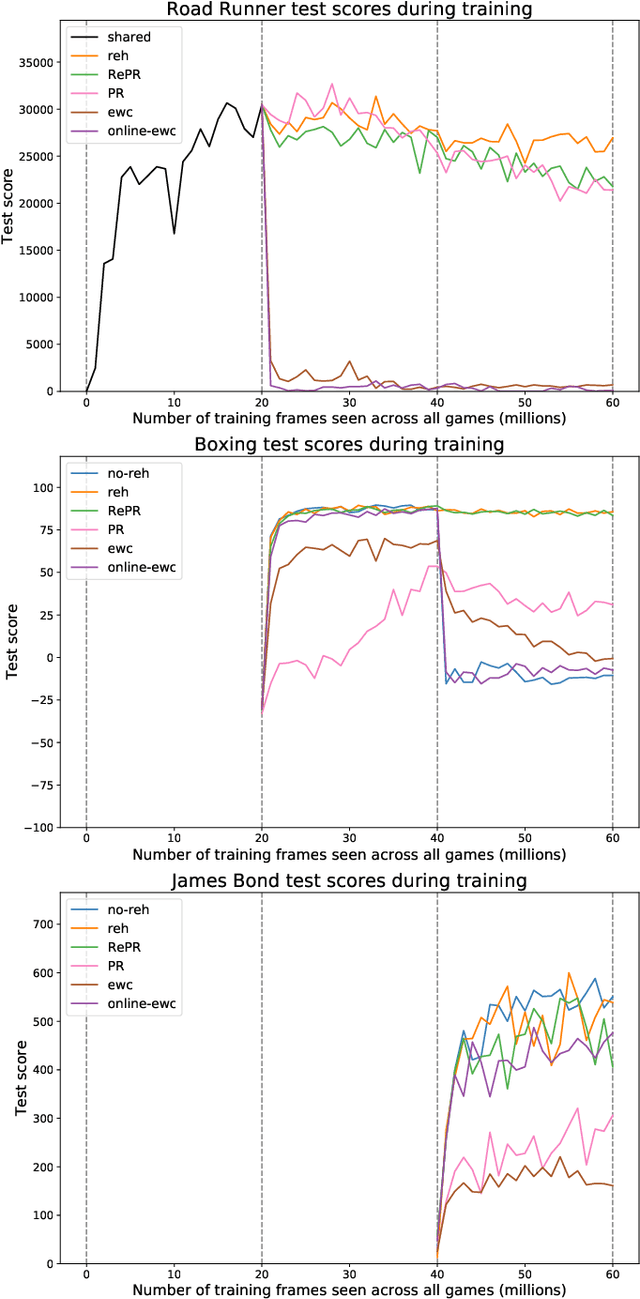
Neural networks can achieve extraordinary results on a wide variety of tasks. However, when they attempt to sequentially learn a number of tasks, they tend to learn the new task while destructively forgetting previous tasks. One solution to this problem is pseudo-rehearsal, which involves learning the new task while rehearsing generated items representative of previous task/s. We demonstrate that pairing pseudo-rehearsal methods with a generative network is an effective solution to this problem in reinforcement learning. Our method iteratively learns three Atari 2600 games while retaining above human level performance on all three games, performing similar to a network which rehearses real examples from all previously learnt tasks.

The effect of the choice of neural network depth and breadth on the size of its hypothesis space

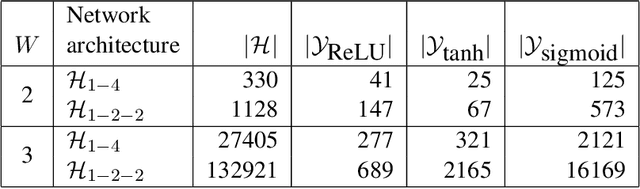
We show that the number of unique function mappings in a neural network hypothesis space is inversely proportional to $\prod_lU_l!$, where $U_{l}$ is the number of neurons in the hidden layer $l$.

Pseudo-Recursal: Solving the Catastrophic Forgetting Problem in Deep Neural Networks

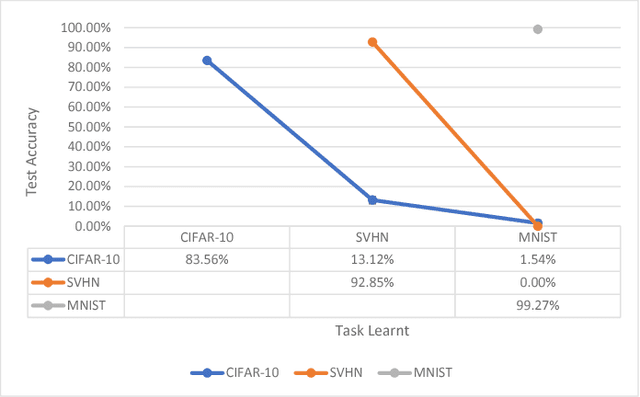
In general, neural networks are not currently capable of learning tasks in a sequential fashion. When a novel, unrelated task is learnt by a neural network, it substantially forgets how to solve previously learnt tasks. One of the original solutions to this problem is pseudo-rehearsal, which involves learning the new task while rehearsing generated items representative of the previous task/s. This is very effective for simple tasks. However, pseudo-rehearsal has not yet been successfully applied to very complex tasks because in these tasks it is difficult to generate representative items. We accomplish pseudo-rehearsal by using a Generative Adversarial Network to generate items so that our deep network can learn to sequentially classify the CIFAR-10, SVHN and MNIST datasets. After training on all tasks, our network loses only 1.67% absolute accuracy on CIFAR-10 and gains 0.24% absolute accuracy on SVHN. Our model's performance is a substantial improvement compared to the current state of the art solution.

Some Approximation Bounds for Deep Networks

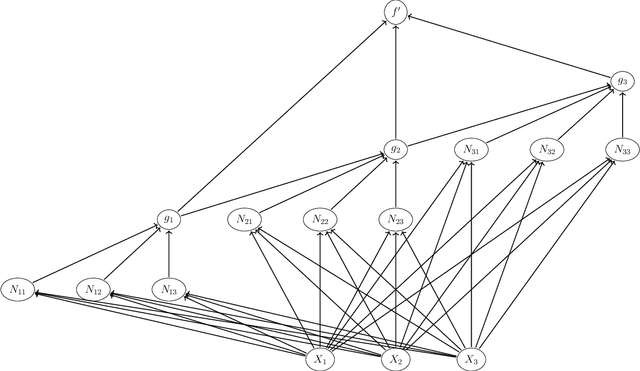
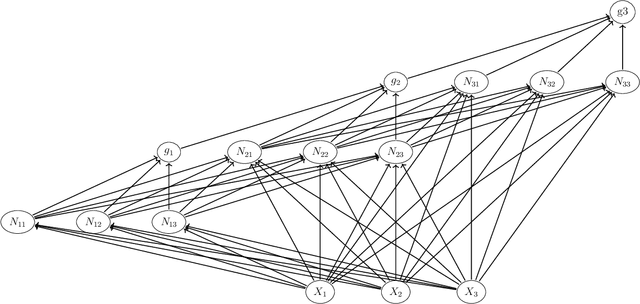
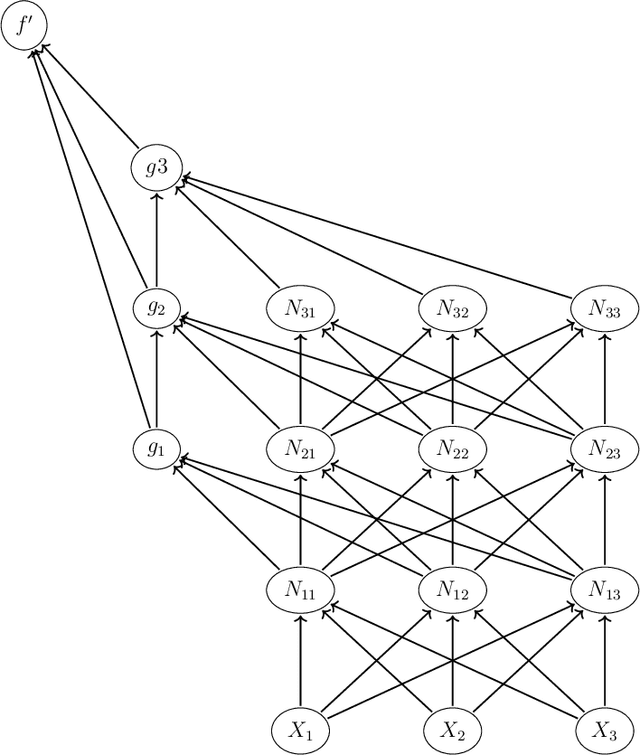
In this paper we introduce new bounds on the approximation of functions in deep networks and in doing so introduce some new deep network architectures for function approximation. These results give some theoretical insight into the success of autoencoders and ResNets.