Michael Albert
Learning in Online Principal-Agent Interactions: The Power of Menus
Dec 28, 2023Abstract:We study a ubiquitous learning challenge in online principal-agent problems during which the principal learns the agent's private information from the agent's revealed preferences in historical interactions. This paradigm includes important special cases such as pricing and contract design, which have been widely studied in recent literature. However, existing work considers the case where the principal can only choose a single strategy at every round to interact with the agent and then observe the agent's revealed preference through their actions. In this paper, we extend this line of study to allow the principal to offer a menu of strategies to the agent and learn additionally from observing the agent's selection from the menu. We provide a thorough investigation of several online principal-agent problem settings and characterize their sample complexities, accompanied by the corresponding algorithms we have developed. We instantiate this paradigm to several important design problems $-$ including Stackelberg (security) games, contract design, and information design. Finally, we also explore the connection between our findings and existing results about online learning in Stackelberg games, and we offer a solution that can overcome a key hard instance of Peng et al. (2019).
The effect of the choice of neural network depth and breadth on the size of its hypothesis space
Jun 06, 2018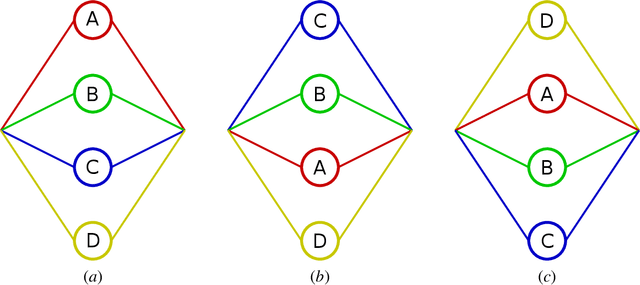
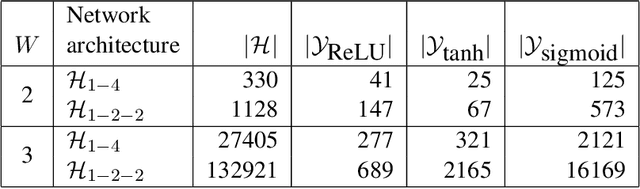

Abstract:We show that the number of unique function mappings in a neural network hypothesis space is inversely proportional to $\prod_lU_l!$, where $U_{l}$ is the number of neurons in the hidden layer $l$.
Traffic Optimization For a Mixture of Self-interested and Compliant Agents
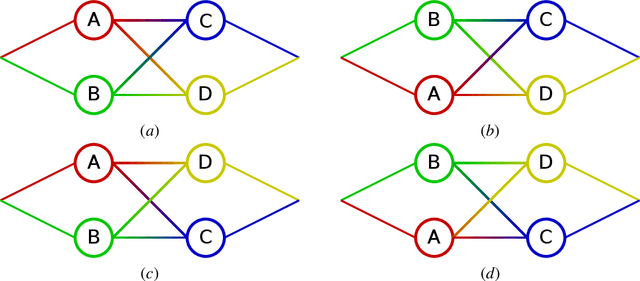
Sep 27, 2017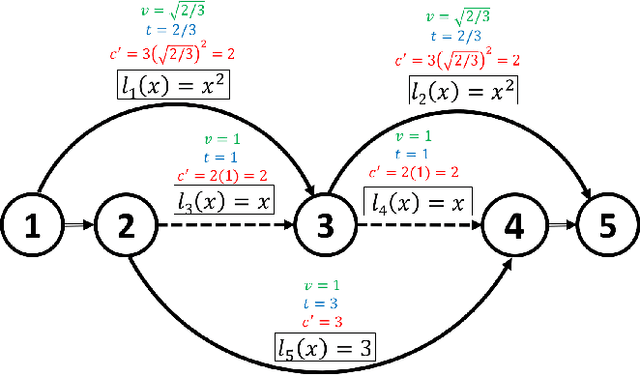

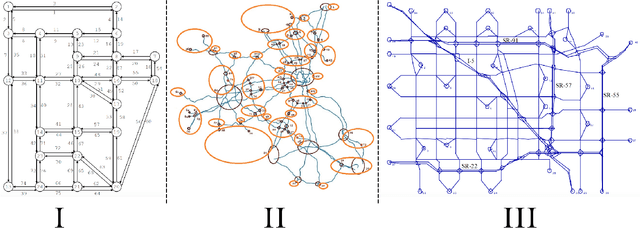
Abstract:This paper focuses on two commonly used path assignment policies for agents traversing a congested network: self-interested routing, and system-optimum routing. In the self-interested routing policy each agent selects a path that optimizes its own utility, while the system-optimum routing agents are assigned paths with the goal of maximizing system performance. This paper considers a scenario where a centralized network manager wishes to optimize utilities over all agents, i.e., implement a system-optimum routing policy. In many real-life scenarios, however, the system manager is unable to influence the route assignment of all agents due to limited influence on route choice decisions. Motivated by such scenarios, a computationally tractable method is presented that computes the minimal amount of agents that the system manager needs to influence (compliant agents) in order to achieve system optimal performance. Moreover, this methodology can also determine whether a given set of compliant agents is sufficient to achieve system optimum and compute the optimal route assignment for the compliant agents to do so. Experimental results are presented showing that in several large-scale, realistic traffic networks optimal flow can be achieved with as low as 13% of the agent being compliant and up to 54%.
Complexity of Scheduling Charging in the Smart Grid
Sep 21, 2017


Abstract:In the smart grid, the intent is to use flexibility in demand, both to balance demand and supply as well as to resolve potential congestion. A first prominent example of such flexible demand is the charging of electric vehicles, which do not necessarily need to be charged as soon as they are plugged in. The problem of optimally scheduling the charging demand of electric vehicles within the constraints of the electricity infrastructure is called the charge scheduling problem. The models of the charging speed, horizon, and charging demand determine the computational complexity of the charge scheduling problem. For about 20 variants, we show, using a dynamic programming approach, that the problem is either in P or weakly NP-hard. We also show that about 10 variants of the problem are strongly NP-hard, presenting a potentially significant obstacle to their use in practical situations of scale.
Auto-JacoBin: Auto-encoder Jacobian Binary Hashing
Mar 01, 2016



Abstract:Binary codes can be used to speed up nearest neighbor search tasks in large scale data sets as they are efficient for both storage and retrieval. In this paper, we propose a robust auto-encoder model that preserves the geometric relationships of high-dimensional data sets in Hamming space. This is done by considering a noise-removing function in a region surrounding the manifold where the training data points lie. This function is defined with the property that it projects the data points near the manifold into the manifold wisely, and we approximate this function by its first order approximation. Experimental results show that the proposed method achieves better than state-of-the-art results on three large scale high dimensional data sets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge