Point Tracking in Surgery--The 2024 Surgical Tattoos in Infrared (STIR) Challenge

Understanding tissue motion in surgery is crucial to enable applications in downstream tasks such as segmentation, 3D reconstruction, virtual tissue landmarking, autonomous probe-based scanning, and subtask autonomy. Labeled data are essential to enabling algorithms in these downstream tasks since they allow us to quantify and train algorithms. This paper introduces a point tracking challenge to address this, wherein participants can submit their algorithms for quantification. The submitted algorithms are evaluated using a dataset named surgical tattoos in infrared (STIR), with the challenge aptly named the STIR Challenge 2024. The STIR Challenge 2024 comprises two quantitative components: accuracy and efficiency. The accuracy component tests the accuracy of algorithms on in vivo and ex vivo sequences. The efficiency component tests the latency of algorithm inference. The challenge was conducted as a part of MICCAI EndoVis 2024. In this challenge, we had 8 total teams, with 4 teams submitting before and 4 submitting after challenge day. This paper details the STIR Challenge 2024, which serves to move the field towards more accurate and efficient algorithms for spatial understanding in surgery. In this paper we summarize the design, submissions, and results from the challenge. The challenge dataset is available here: https://zenodo.org/records/14803158 , and the code for baseline models and metric calculation is available here: https://github.com/athaddius/STIRMetrics

Adaptive Graduated Nonconvexity Loss

Many problems in robotics, such as estimating the state from noisy sensor data or aligning two LiDAR point clouds, can be posed and solved as least-squares problems. Unfortunately, vanilla nonminimal solvers for least-squares problems are notoriously sensitive to outliers. As such, various robust loss functions have been proposed to reduce the sensitivity to outliers. Examples of loss functions include pseudo-Huber, Cauchy, and Geman-McClure. Recently, these loss functions have been generalized into a single loss function that enables the best loss function to be found adaptively based on the distribution of the residuals. However, even with the generalized robust loss function, most nonminimal solvers can only be solved locally given a prior state estimate due to the nonconvexity of the problem. The first contribution of this paper is to combine graduated nonconvexity (GNC) with the generalized robust loss function to solve least-squares problems without a prior state estimate and without the need to specify a loss function. Moreover, existing loss functions, including the generalized loss function, are based on Gaussian-like distribution. However, residuals are often defined as the squared norm of a multivariate error and distributed in a Chi-like fashion. The second contribution of this paper is to apply a norm-aware adaptive robust loss function within a GNC framework. This leads to additional robustness when compared with state-of-the-art methods. Simulations and experiments demonstrate that the proposed approach is more robust and yields faster convergence times compared to other GNC formulations.

Performance Evaluation of 3D Keypoint Detectors and Descriptors on Coloured Point Clouds in Subsea Environments

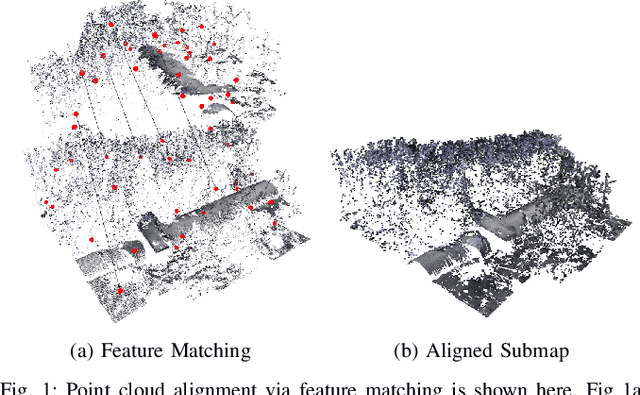
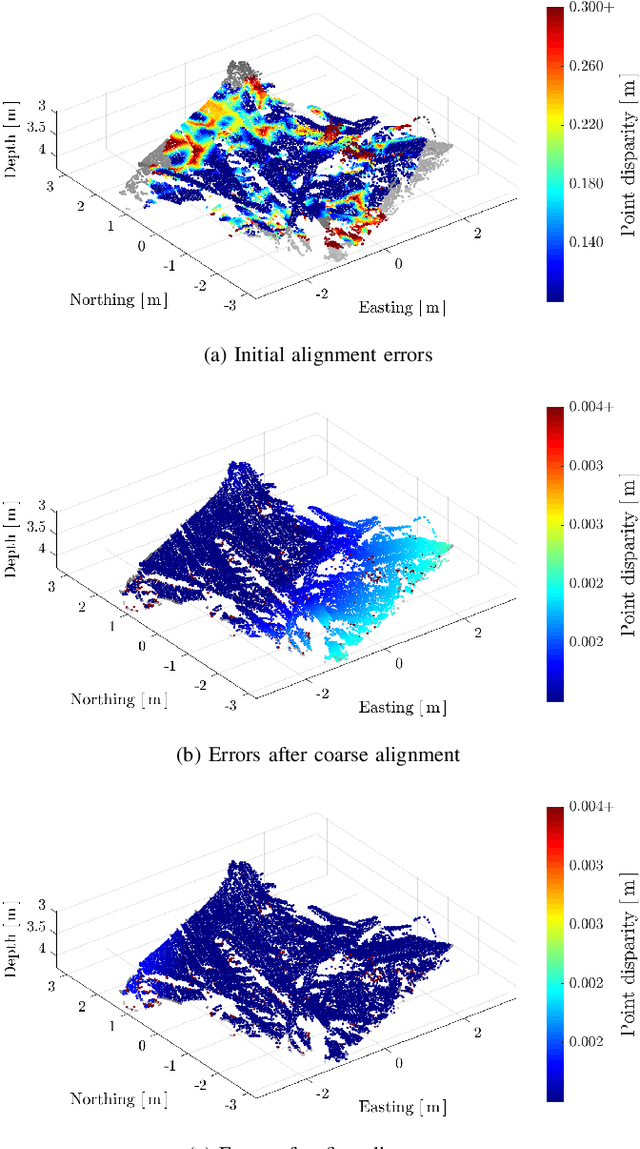
The recent development of high-precision subsea optical scanners allows for 3D keypoint detectors and feature descriptors to be leveraged on point cloud scans from subsea environments. However, the literature lacks a comprehensive survey to identify the best combination of detectors and descriptors to be used in these challenging and novel environments. This paper aims to identify the best detector/descriptor pair using a challenging field dataset collected using a commercial underwater laser scanner. Furthermore, studies have shown that incorporating texture information to extend geometric features adds robustness to feature matching on synthetic datasets. This paper also proposes a novel method of fusing images with underwater laser scans to produce coloured point clouds, which are used to study the effectiveness of 6D point cloud descriptors.