Peering Partner Recommendation for ISPs using Machine Learning

Internet service providers (ISPs) need to connect with other ISPs to provide global connectivity services to their users. To ensure global connectivity, ISPs can either use transit service(s) or establish direct peering relationships between themselves via Internet exchange points (IXPs). Peering offers more room for ISP-specific optimizations and is preferred, but it often involves a lengthy and complex process. Automating peering partner selection can enhance efficiency in the global Internet ecosystem. We explore the use of publicly available data on ISPs to develop a machine learning (ML) model that can predict whether an ISP pair should peer or not. At first, we explore public databases, e.g., PeeringDB, CAIDA, etc., to gather data on ISPs. Then, we evaluate the performance of three broad types of ML models for predicting peering relationships: tree-based, neural network-based, and transformer-based. Among these, we observe that tree-based models achieve the highest accuracy and efficiency in our experiments. The XGBoost model trained with publicly available data showed promising performance, with a 98% accuracy rate in predicting peering partners. In addition, the model demonstrated great resilience to variations in time, space, and missing data. We envision that ISPs can adopt our method to fully automate the peering partner selection process, thus transitioning to a more efficient and optimized Internet ecosystem.

Leveraging Large Language Models for Wireless Symbol Detection via In-Context Learning

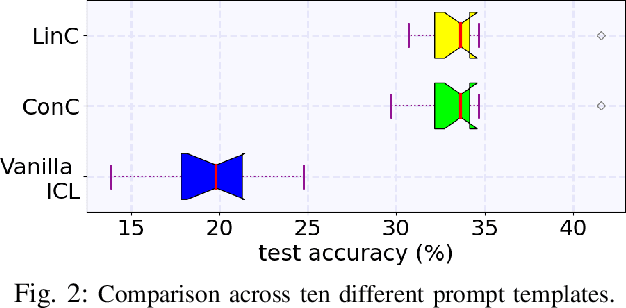
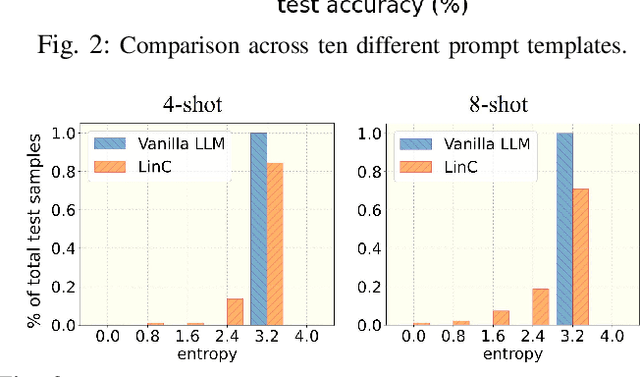
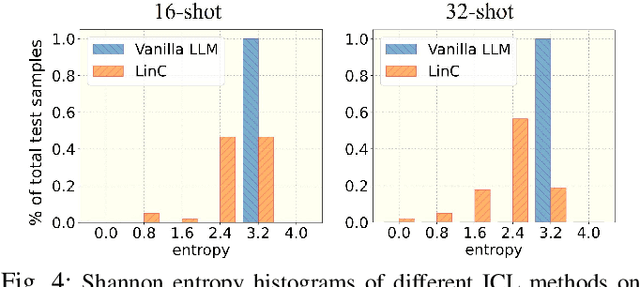
Deep neural networks (DNNs) have made significant strides in tackling challenging tasks in wireless systems, especially when an accurate wireless model is not available. However, when available data is limited, traditional DNNs often yield subpar results due to underfitting. At the same time, large language models (LLMs) exemplified by GPT-3, have remarkably showcased their capabilities across a broad range of natural language processing tasks. But whether and how LLMs can benefit challenging non-language tasks in wireless systems is unexplored. In this work, we propose to leverage the in-context learning ability (a.k.a. prompting) of LLMs to solve wireless tasks in the low data regime without any training or fine-tuning, unlike DNNs which require training. We further demonstrate that the performance of LLMs varies significantly when employed with different prompt templates. To solve this issue, we employ the latest LLM calibration methods. Our results reveal that using LLMs via ICL methods generally outperforms traditional DNNs on the symbol demodulation task and yields highly confident predictions when coupled with calibration techniques.

On the Utility of Domain-Adjacent Fine-Tuned Model Ensembles for Few-shot Problems

Large Language Models (LLMs) have been observed to perform well on a wide range of downstream tasks when fine-tuned on domain-specific data. However, such data may not be readily available in many applications, motivating zero-shot or few-shot approaches using domain-adjacent models. While several fine-tuned models for various tasks are available, finding an appropriate domain-adjacent model for a given task is often not straight forward. In this paper, we study DAFT-E, a framework that utilizes an Ensemble of Domain-Adjacent Fine-Tuned Foundation Models for few-shot problems. We show that for zero-shot problems, this ensembling method provides an accuracy performance close to that of the single best model. With few-shot problems, this performance improves further, at which point DEFT-E can outperform any single domain-adjacent model while requiring much less data for domain-specific fine-tuning.

Adaptive Primal-Dual Method for Safe Reinforcement Learning

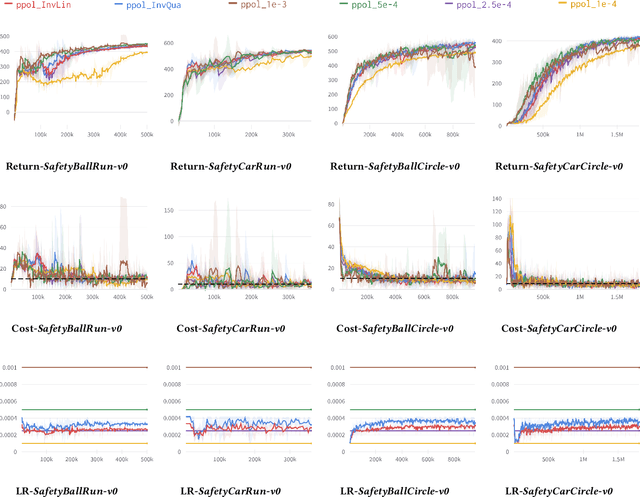
Primal-dual methods have a natural application in Safe Reinforcement Learning (SRL), posed as a constrained policy optimization problem. In practice however, applying primal-dual methods to SRL is challenging, due to the inter-dependency of the learning rate (LR) and Lagrangian multipliers (dual variables) each time an embedded unconstrained RL problem is solved. In this paper, we propose, analyze and evaluate adaptive primal-dual (APD) methods for SRL, where two adaptive LRs are adjusted to the Lagrangian multipliers so as to optimize the policy in each iteration. We theoretically establish the convergence, optimality and feasibility of the APD algorithm. Finally, we conduct numerical evaluation of the practical APD algorithm with four well-known environments in Bullet-Safey-Gym employing two state-of-the-art SRL algorithms: PPO-Lagrangian and DDPG-Lagrangian. All experiments show that the practical APD algorithm outperforms (or achieves comparable performance) and attains more stable training than the constant LR cases. Additionally, we substantiate the robustness of selecting the two adaptive LRs by empirical evidence.