Autonomous helicopter aerial refueling: controller design and performance guarantees

In this paper, we present a control design methodology, stability criteria, and performance bounds for autonomous helicopter aerial refueling. Autonomous aerial refueling is particularly difficult due to the aerodynamic interaction between the wake of the tanker, the contact-sensitive nature of the maneuver, and the uncertainty in drogue motion. Since the probe tip is located significantly away from the helicopter's center-of-gravity, its position (and velocity) is strongly sensitive to the helicopter's attitude (and angular rates). In addition, the fact that the helicopter is operating at high speeds to match the velocity of the tanker forces it to maintain a particular orientation, making the docking maneuver especially challenging. In this paper, we propose a novel outer-loop position controller that incorporates the probe position and velocity into the feedback loop. The position and velocity of the probe tip depend both on the position (velocity) and on the attitude (angular rates) of the aircraft. We derive analytical guarantees for docking performance in terms of the uncertainty of the drogue motion and the angular acceleration of the helicopter, using the ultimate boundedness property of the closed-loop error dynamics. Simulations are performed on a high-fidelity UH60 helicopter model with a high-fidelity drogue motion under wind effects to validate the proposed approach for realistic refueling scenarios. These high-fidelity simulations reveal that the proposed control methodology yields an improvement of 36% in the 2-norm docking error compared to the existing standard controller.

Robotic Wire Arc Additive Manufacturing with Variable Height Layers

Robotic wire arc additive manufacturing has been widely adopted due to its high deposition rates and large print volume relative to other metal additive manufacturing processes. For complex geometries, printing with variable height within layers offer the advantage of producing overhangs without the need for support material or geometric decomposition. This approach has been demonstrated for steel using precomputed robot speed profiles to achieve consistent geometric quality. In contrast, aluminum exhibits a bead geometry that is tightly coupled to the temperature of the previous layer, resulting in significant changes to the height of the deposited material at different points in the part. This paper presents a closed-loop approach to correcting for variations in the height of the deposited material between layers. We use an IR camera mounted on a separate robot to track the welding flame and estimate the height of deposited material. The robot velocity profile is then updated to account for the error in the previous layer and the nominal planned height profile while factoring in process and system constraints. Implementation of this framework showed significant improvement over the open-loop case and demonstrated robustness to inaccurate model parameters.

Transfer Learning for a Class of Cascade Dynamical Systems

This work considers the problem of transfer learning in the context of reinforcement learning. Specifically, we consider training a policy in a reduced order system and deploying it in the full state system. The motivation for this training strategy is that running simulations in the full-state system may take excessive time if the dynamics are complex. While transfer learning alleviates the computational issue, the transfer guarantees depend on the discrepancy between the two systems. In this work, we consider a class of cascade dynamical systems, where the dynamics of a subset of the state-space influence the rest of the states but not vice-versa. The reinforcement learning policy learns in a model that ignores the dynamics of these states and treats them as commanded inputs. In the full-state system, these dynamics are handled using a classic controller (e.g., a PID). These systems have vast applications in the control literature and their structure allows us to provide transfer guarantees that depend on the stability of the inner loop controller. Numerical experiments on a quadrotor support the theoretical findings.

Domain Adaptation for Offline Reinforcement Learning with Limited Samples

Offline reinforcement learning (RL) learns effective policies from a static target dataset. Despite state-of-the-art (SOTA) offline RL algorithms being promising, they highly rely on the quality of the target dataset. The performance of SOTA algorithms can degrade in scenarios with limited samples in the target dataset, which is often the case in real-world applications. To address this issue, domain adaptation that leverages auxiliary samples from related source datasets (such as simulators) can be beneficial. In this context, determining the optimal way to trade off the source and target datasets remains a critical challenge in offline RL. To the best of our knowledge, this paper proposes the first framework that theoretically and experimentally explores how the weight assigned to each dataset affects the performance of offline RL. We establish the performance bounds and convergence neighborhood of our framework, both of which depend on the selection of the weight. Furthermore, we identify the existence of an optimal weight for balancing the two datasets. All theoretical guarantees and optimal weight depend on the quality of the source dataset and the size of the target dataset. Our empirical results on the well-known Procgen Benchmark substantiate our theoretical contributions.

Adaptive Primal-Dual Method for Safe Reinforcement Learning

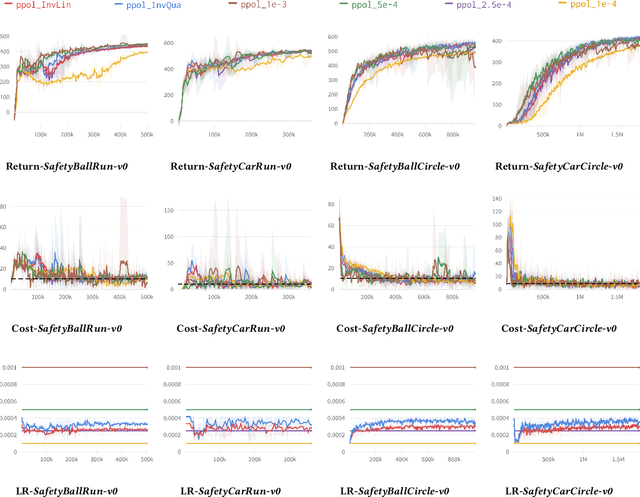
Primal-dual methods have a natural application in Safe Reinforcement Learning (SRL), posed as a constrained policy optimization problem. In practice however, applying primal-dual methods to SRL is challenging, due to the inter-dependency of the learning rate (LR) and Lagrangian multipliers (dual variables) each time an embedded unconstrained RL problem is solved. In this paper, we propose, analyze and evaluate adaptive primal-dual (APD) methods for SRL, where two adaptive LRs are adjusted to the Lagrangian multipliers so as to optimize the policy in each iteration. We theoretically establish the convergence, optimality and feasibility of the APD algorithm. Finally, we conduct numerical evaluation of the practical APD algorithm with four well-known environments in Bullet-Safey-Gym employing two state-of-the-art SRL algorithms: PPO-Lagrangian and DDPG-Lagrangian. All experiments show that the practical APD algorithm outperforms (or achieves comparable performance) and attains more stable training than the constant LR cases. Additionally, we substantiate the robustness of selecting the two adaptive LRs by empirical evidence.