An Operator Splitting View of Federated Learning

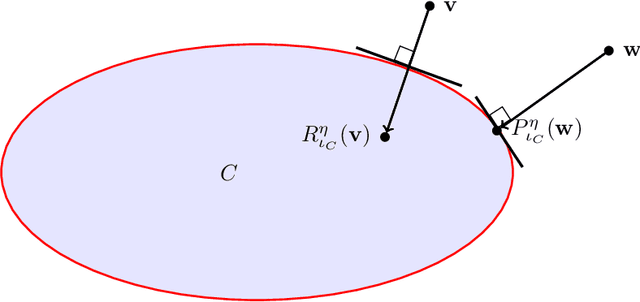
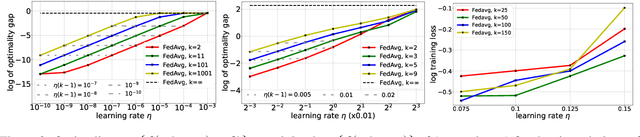
Over the past few years, the federated learning ($\texttt{FL}$) community has witnessed a proliferation of new $\texttt{FL}$ algorithms. However, our understating of the theory of $\texttt{FL}$ is still fragmented, and a thorough, formal comparison of these algorithms remains elusive. Motivated by this gap, we show that many of the existing $\texttt{FL}$ algorithms can be understood from an operator splitting point of view. This unification allows us to compare different algorithms with ease, to refine previous convergence results and to uncover new algorithmic variants. In particular, our analysis reveals the vital role played by the step size in $\texttt{FL}$ algorithms. The unification also leads to a streamlined and economic way to accelerate $\texttt{FL}$ algorithms, without incurring any communication overhead. We perform numerical experiments on both convex and nonconvex models to validate our findings.

FedMGDA+: Federated Learning meets Multi-objective Optimization

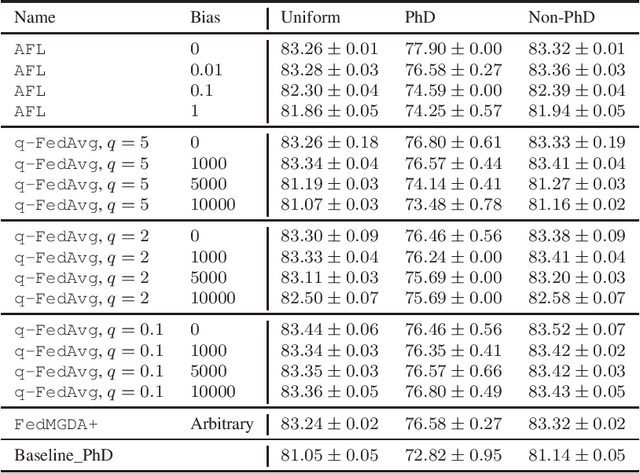
Federated learning has emerged as a promising, massively distributed way to train a joint deep model over large amounts of edge devices while keeping private user data strictly on device. In this work, motivated from ensuring fairness among users and robustness against malicious adversaries, we formulate federated learning as multi-objective optimization and propose a new algorithm FedMGDA+ that is guaranteed to converge to Pareto stationary solutions. FedMGDA+ is simple to implement, has fewer hyperparameters to tune, and refrains from sacrificing the performance of any participating user. We establish the convergence properties of FedMGDA+ and point out its connections to existing approaches. Extensive experiments on a variety of datasets confirm that FedMGDA+ compares favorably against state-of-the-art.

Adaptive MCMC via Combining Local Samplers

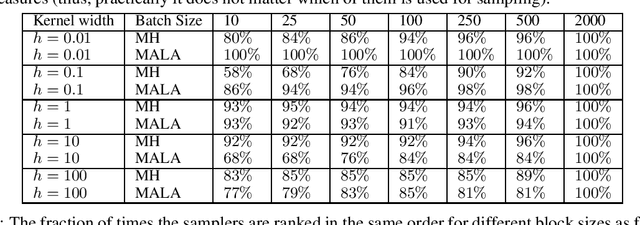
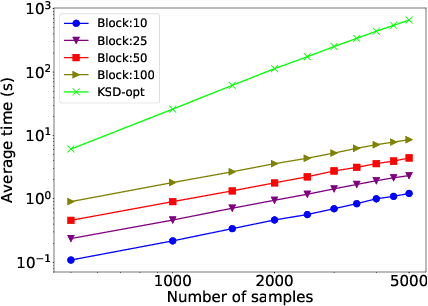
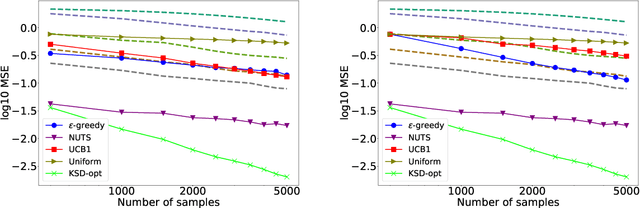
Markov chain Monte Carlo (MCMC) methods are widely used in machine learning. One of the major problems with MCMC is the question of how to design chains that mix fast over the whole space; in particular, how to select the parameters of an MCMC algorithm. Here we take a different approach and, instead of trying to find a single chain to sample from the whole distribution, we combine samples from several chains run in parallel, each exploring only a few modes. The chains are prioritized based on Stein discrepancy, which provides a good measure of performance locally. We present a new method, based on estimating the R\'enyi entropy of subsets of the samples, to combine the samples coming from the different samplers. The resulting algorithm is asymptotically consistent and may lead to significant speedups, especially for multimodal target functions, as demonstrated by our experiments.

SDP Relaxation with Randomized Rounding for Energy Disaggregation

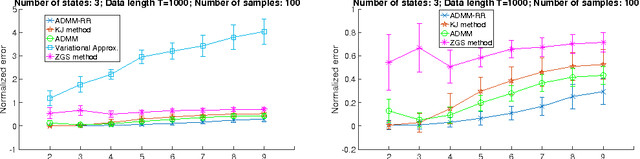
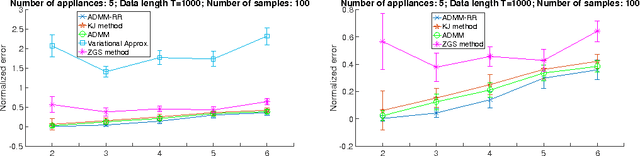
We develop a scalable, computationally efficient method for the task of energy disaggregation for home appliance monitoring. In this problem the goal is to estimate the energy consumption of each appliance over time based on the total energy-consumption signal of a household. The current state of the art is to model the problem as inference in factorial HMMs, and use quadratic programming to find an approximate solution to the resulting quadratic integer program. Here we take a more principled approach, better suited to integer programming problems, and find an approximate optimum by combining convex semidefinite relaxations randomized rounding, as well as a scalable ADMM method that exploits the special structure of the resulting semidefinite program. Simulation results both in synthetic and real-world datasets demonstrate the superiority of our method.