An Operator Splitting View of Federated Learning

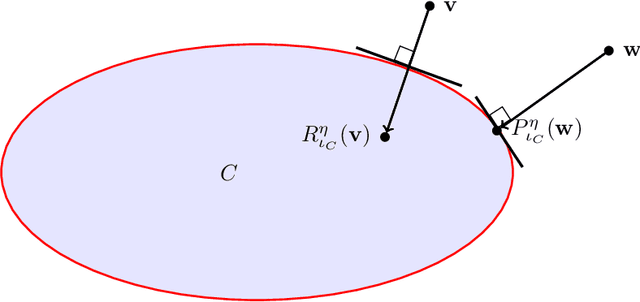
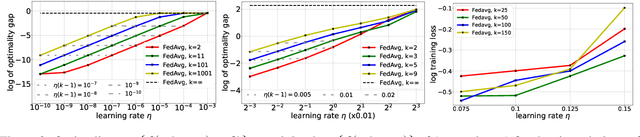
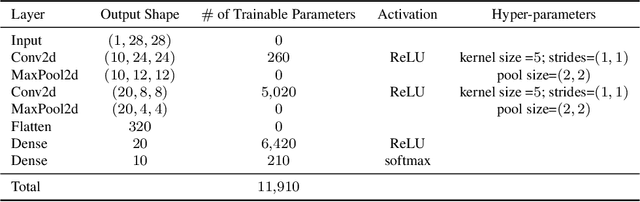
Over the past few years, the federated learning ($\texttt{FL}$) community has witnessed a proliferation of new $\texttt{FL}$ algorithms. However, our understating of the theory of $\texttt{FL}$ is still fragmented, and a thorough, formal comparison of these algorithms remains elusive. Motivated by this gap, we show that many of the existing $\texttt{FL}$ algorithms can be understood from an operator splitting point of view. This unification allows us to compare different algorithms with ease, to refine previous convergence results and to uncover new algorithmic variants. In particular, our analysis reveals the vital role played by the step size in $\texttt{FL}$ algorithms. The unification also leads to a streamlined and economic way to accelerate $\texttt{FL}$ algorithms, without incurring any communication overhead. We perform numerical experiments on both convex and nonconvex models to validate our findings.

FedMGDA+: Federated Learning meets Multi-objective Optimization

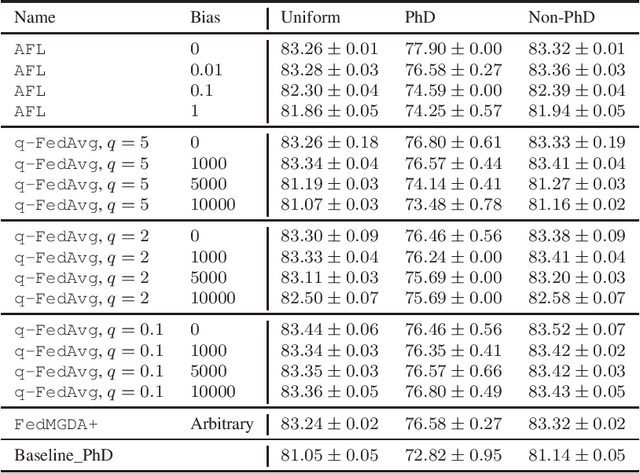
Federated learning has emerged as a promising, massively distributed way to train a joint deep model over large amounts of edge devices while keeping private user data strictly on device. In this work, motivated from ensuring fairness among users and robustness against malicious adversaries, we formulate federated learning as multi-objective optimization and propose a new algorithm FedMGDA+ that is guaranteed to converge to Pareto stationary solutions. FedMGDA+ is simple to implement, has fewer hyperparameters to tune, and refrains from sacrificing the performance of any participating user. We establish the convergence properties of FedMGDA+ and point out its connections to existing approaches. Extensive experiments on a variety of datasets confirm that FedMGDA+ compares favorably against state-of-the-art.