An Operator Splitting View of Federated Learning
Paper and Code
Aug 12, 2021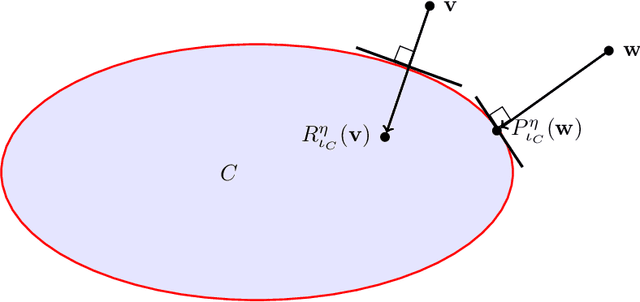
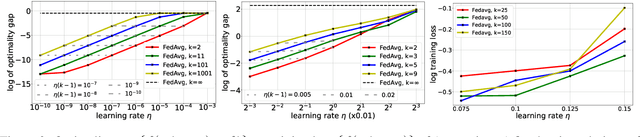
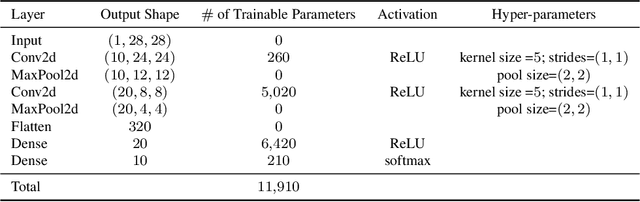

Over the past few years, the federated learning ($\texttt{FL}$) community has witnessed a proliferation of new $\texttt{FL}$ algorithms. However, our understating of the theory of $\texttt{FL}$ is still fragmented, and a thorough, formal comparison of these algorithms remains elusive. Motivated by this gap, we show that many of the existing $\texttt{FL}$ algorithms can be understood from an operator splitting point of view. This unification allows us to compare different algorithms with ease, to refine previous convergence results and to uncover new algorithmic variants. In particular, our analysis reveals the vital role played by the step size in $\texttt{FL}$ algorithms. The unification also leads to a streamlined and economic way to accelerate $\texttt{FL}$ algorithms, without incurring any communication overhead. We perform numerical experiments on both convex and nonconvex models to validate our findings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge