Adaptive MCMC via Combining Local Samplers

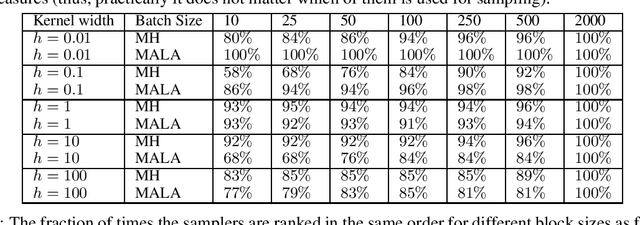
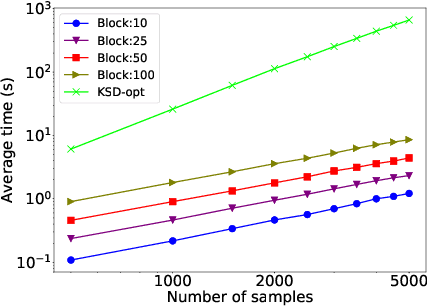
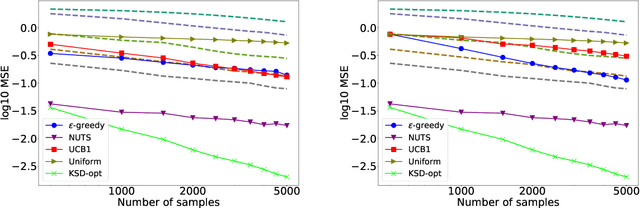
Markov chain Monte Carlo (MCMC) methods are widely used in machine learning. One of the major problems with MCMC is the question of how to design chains that mix fast over the whole space; in particular, how to select the parameters of an MCMC algorithm. Here we take a different approach and, instead of trying to find a single chain to sample from the whole distribution, we combine samples from several chains run in parallel, each exploring only a few modes. The chains are prioritized based on Stein discrepancy, which provides a good measure of performance locally. We present a new method, based on estimating the R\'enyi entropy of subsets of the samples, to combine the samples coming from the different samplers. The resulting algorithm is asymptotically consistent and may lead to significant speedups, especially for multimodal target functions, as demonstrated by our experiments.