The Problem of Social Cost in Multi-Agent General Reinforcement Learning: Survey and Synthesis

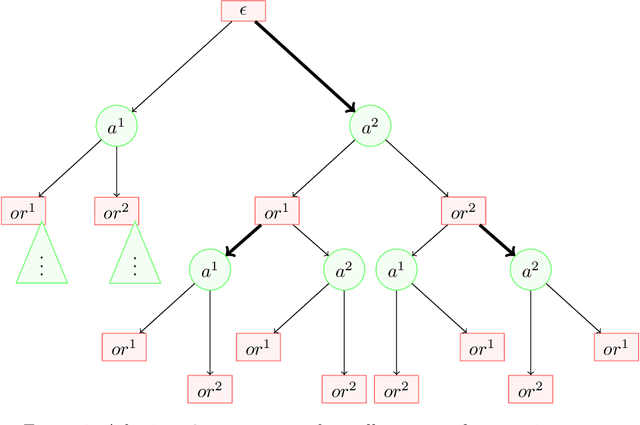
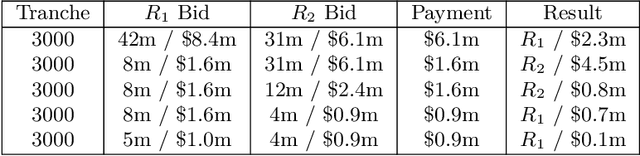
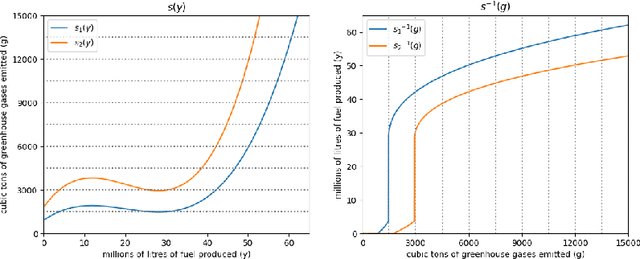
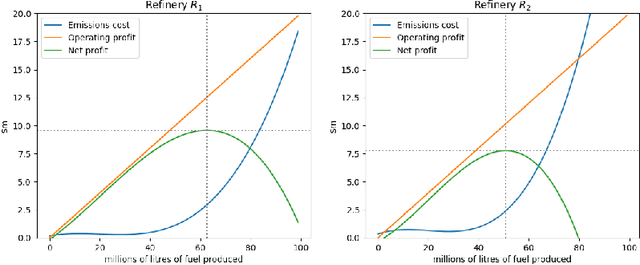
The AI safety literature is full of examples of powerful AI agents that, in blindly pursuing a specific and usually narrow objective, ends up with unacceptable and even catastrophic collateral damage to others. In this paper, we consider the problem of social harms that can result from actions taken by learning and utility-maximising agents in a multi-agent environment. The problem of measuring social harms or impacts in such multi-agent settings, especially when the agents are artificial generally intelligent (AGI) agents, was listed as an open problem in Everitt et al, 2018. We attempt a partial answer to that open problem in the form of market-based mechanisms to quantify and control the cost of such social harms. The proposed setup captures many well-studied special cases and is more general than existing formulations of multi-agent reinforcement learning with mechanism design in two ways: (i) the underlying environment is a history-based general reinforcement learning environment like in AIXI; (ii) the reinforcement-learning agents participating in the environment can have different learning strategies and planning horizons. To demonstrate the practicality of the proposed setup, we survey some key classes of learning algorithms and present a few applications, including a discussion of the Paperclips problem and pollution control with a cap-and-trade system.

Privacy Preserving Reinforcement Learning for Population Processes

We consider the problem of privacy protection in Reinforcement Learning (RL) algorithms that operate over population processes, a practical but understudied setting that includes, for example, the control of epidemics in large populations of dynamically interacting individuals. In this setting, the RL algorithm interacts with the population over $T$ time steps by receiving population-level statistics as state and performing actions which can affect the entire population at each time step. An individual's data can be collected across multiple interactions and their privacy must be protected at all times. We clarify the Bayesian semantics of Differential Privacy (DP) in the presence of correlated data in population processes through a Pufferfish Privacy analysis. We then give a meta algorithm that can take any RL algorithm as input and make it differentially private. This is achieved by taking an approach that uses DP mechanisms to privatize the state and reward signal at each time step before the RL algorithm receives them as input. Our main theoretical result shows that the value-function approximation error when applying standard RL algorithms directly to the privatized states shrinks quickly as the population size and privacy budget increase. This highlights that reasonable privacy-utility trade-offs are possible for differentially private RL algorithms in population processes. Our theoretical findings are validated by experiments performed on a simulated epidemic control problem over large population sizes.

Dynamic Knowledge Injection for AIXI Agents

Prior approximations of AIXI, a Bayesian optimality notion for general reinforcement learning, can only approximate AIXI's Bayesian environment model using an a-priori defined set of models. This is a fundamental source of epistemic uncertainty for the agent in settings where the existence of systematic bias in the predefined model class cannot be resolved by simply collecting more data from the environment. We address this issue in the context of Human-AI teaming by considering a setup where additional knowledge for the agent in the form of new candidate models arrives from a human operator in an online fashion. We introduce a new agent called DynamicHedgeAIXI that maintains an exact Bayesian mixture over dynamically changing sets of models via a time-adaptive prior constructed from a variant of the Hedge algorithm. The DynamicHedgeAIXI agent is the richest direct approximation of AIXI known to date and comes with good performance guarantees. Experimental results on epidemic control on contact networks validates the agent's practical utility.

Variational Inference for Scalable 3D Object-centric Learning

We tackle the task of scalable unsupervised object-centric representation learning on 3D scenes. Existing approaches to object-centric representation learning show limitations in generalizing to larger scenes as their learning processes rely on a fixed global coordinate system. In contrast, we propose to learn view-invariant 3D object representations in localized object coordinate systems. To this end, we estimate the object pose and appearance representation separately and explicitly map object representations across views while maintaining object identities. We adopt an amortized variational inference pipeline that can process sequential input and scalably update object latent distributions online. To handle large-scale scenes with a varying number of objects, we further introduce a Cognitive Map that allows the registration and query of objects on a per-scene global map to achieve scalable representation learning. We explore the object-centric neural radiance field (NeRF) as our 3D scene representation, which is jointly modeled within our unsupervised object-centric learning framework. Experimental results on synthetic and real datasets show that our proposed method can infer and maintain object-centric representations of 3D scenes and outperforms previous models.

A Direct Approximation of AIXI Using Logical State Abstractions

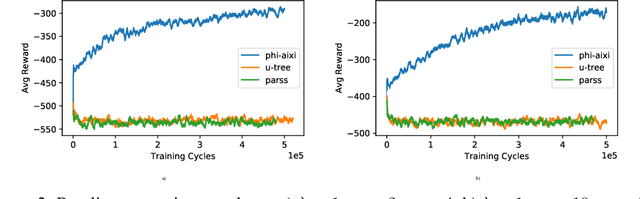
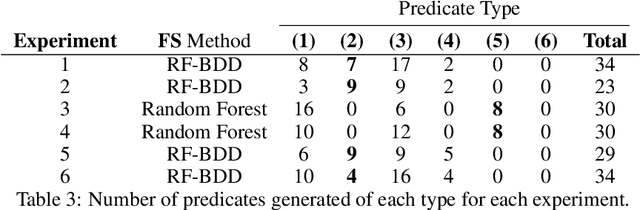
We propose a practical integration of logical state abstraction with AIXI, a Bayesian optimality notion for reinforcement learning agents, to significantly expand the model class that AIXI agents can be approximated over to complex history-dependent and structured environments. The state representation and reasoning framework is based on higher-order logic, which can be used to define and enumerate complex features on non-Markovian and structured environments. We address the problem of selecting the right subset of features to form state abstractions by adapting the $\Phi$-MDP optimisation criterion from state abstraction theory. Exact Bayesian model learning is then achieved using a suitable generalisation of Context Tree Weighting over abstract state sequences. The resultant architecture can be integrated with different planning algorithms. Experimental results on controlling epidemics on large-scale contact networks validates the agent's performance.

Factored Conditional Filtering: Tracking States and Estimating Parameters in High-Dimensional Spaces

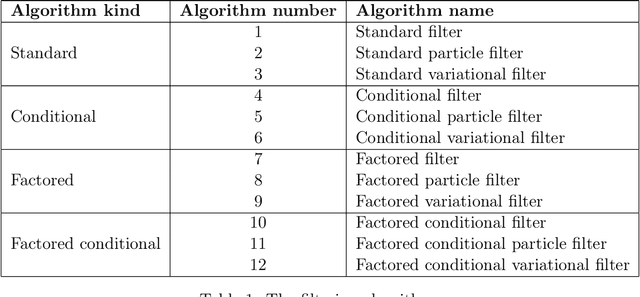
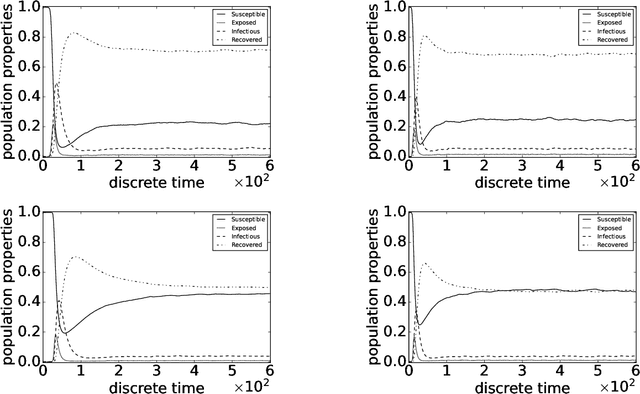
This paper introduces the factored conditional filter, a new filtering algorithm for simultaneously tracking states and estimating parameters in high-dimensional state spaces. The conditional nature of the algorithm is used to estimate parameters and the factored nature is used to decompose the state space into low-dimensional subspaces in such a way that filtering on these subspaces gives distributions whose product is a good approximation to the distribution on the entire state space. The conditions for successful application of the algorithm are that observations be available at the subspace level and that the transition model can be factored into local transition models that are approximately confined to the subspaces; these conditions are widely satisfied in computer science, engineering, and geophysical filtering applications. We give experimental results on tracking epidemics and estimating parameters in large contact networks that show the effectiveness of our approach.

Spatially Invariant Unsupervised 3D Object Segmentation with Graph Neural Networks

In this paper, we tackle the problem of unsupervised 3D object segmentation from a point cloud without RGB information. In particular, we propose a framework, SPAIR3D, to model a point cloud as a spatial mixture model and jointly learn the multiple-object representation and segmentation in 3D via Variational Autoencoders (VAE). Inspired by SPAIR, we adopt an object-specification scheme that describes each object's location relative to its local voxel grid cell rather than the point cloud as a whole. To model the spatial mixture model on point clouds, we derive the Chamfer Likelihood, which fits naturally into the variational training pipeline. We further design a new spatially invariant graph neural network to generate a varying number of 3D points as a decoder within our VAE. Experimental results demonstrate that SPAIR3D is capable of detecting and segmenting variable number of objects without appearance information across diverse scenes.

Probabilities on Sentences in an Expressive Logic

Automated reasoning about uncertain knowledge has many applications. One difficulty when developing such systems is the lack of a completely satisfactory integration of logic and probability. We address this problem directly. Expressive languages like higher-order logic are ideally suited for representing and reasoning about structured knowledge. Uncertain knowledge can be modeled by using graded probabilities rather than binary truth-values. The main technical problem studied in this paper is the following: Given a set of sentences, each having some probability of being true, what probability should be ascribed to other (query) sentences? A natural wish-list, among others, is that the probability distribution (i) is consistent with the knowledge base, (ii) allows for a consistent inference procedure and in particular (iii) reduces to deductive logic in the limit of probabilities being 0 and 1, (iv) allows (Bayesian) inductive reasoning and (v) learning in the limit and in particular (vi) allows confirmation of universally quantified hypotheses/sentences. We translate this wish-list into technical requirements for a prior probability and show that probabilities satisfying all our criteria exist. We also give explicit constructions and several general characterizations of probabilities that satisfy some or all of the criteria and various (counter) examples. We also derive necessary and sufficient conditions for extending beliefs about finitely many sentences to suitable probabilities over all sentences, and in particular least dogmatic or least biased ones. We conclude with a brief outlook on how the developed theory might be used and approximated in autonomous reasoning agents. Our theory is a step towards a globally consistent and empirically satisfactory unification of probability and logic.

A Monte Carlo AIXI Approximation

This paper introduces a principled approach for the design of a scalable general reinforcement learning agent. Our approach is based on a direct approximation of AIXI, a Bayesian optimality notion for general reinforcement learning agents. Previously, it has been unclear whether the theory of AIXI could motivate the design of practical algorithms. We answer this hitherto open question in the affirmative, by providing the first computationally feasible approximation to the AIXI agent. To develop our approximation, we introduce a new Monte-Carlo Tree Search algorithm along with an agent-specific extension to the Context Tree Weighting algorithm. Empirically, we present a set of encouraging results on a variety of stochastic and partially observable domains. We conclude by proposing a number of directions for future research.

Reinforcement Learning via AIXI Approximation

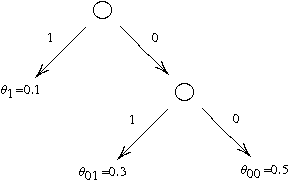
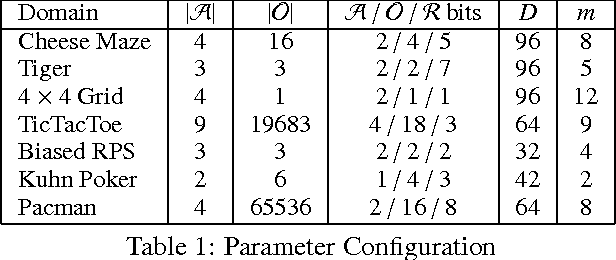
This paper introduces a principled approach for the design of a scalable general reinforcement learning agent. This approach is based on a direct approximation of AIXI, a Bayesian optimality notion for general reinforcement learning agents. Previously, it has been unclear whether the theory of AIXI could motivate the design of practical algorithms. We answer this hitherto open question in the affirmative, by providing the first computationally feasible approximation to the AIXI agent. To develop our approximation, we introduce a Monte Carlo Tree Search algorithm along with an agent-specific extension of the Context Tree Weighting algorithm. Empirically, we present a set of encouraging results on a number of stochastic, unknown, and partially observable domains.