The Problem of Social Cost in Multi-Agent General Reinforcement Learning: Survey and Synthesis

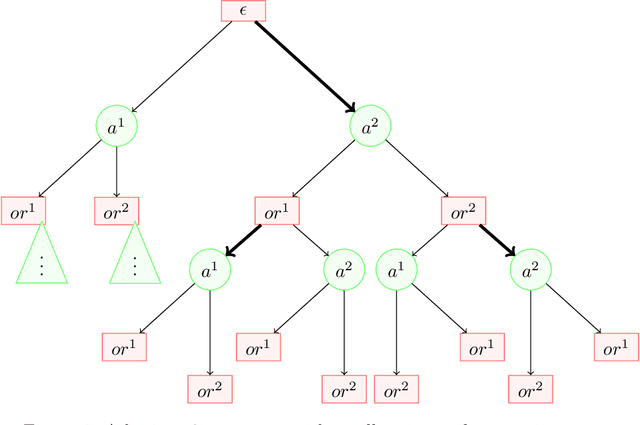
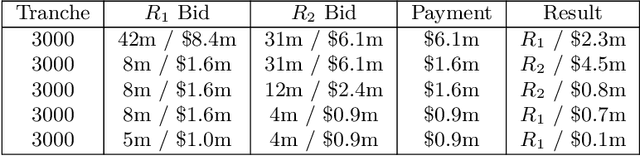
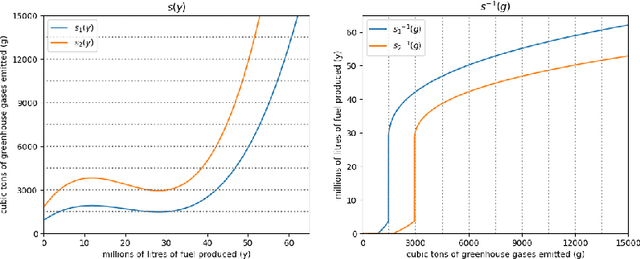
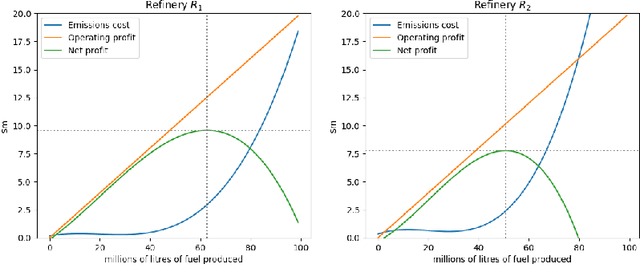
The AI safety literature is full of examples of powerful AI agents that, in blindly pursuing a specific and usually narrow objective, ends up with unacceptable and even catastrophic collateral damage to others. In this paper, we consider the problem of social harms that can result from actions taken by learning and utility-maximising agents in a multi-agent environment. The problem of measuring social harms or impacts in such multi-agent settings, especially when the agents are artificial generally intelligent (AGI) agents, was listed as an open problem in Everitt et al, 2018. We attempt a partial answer to that open problem in the form of market-based mechanisms to quantify and control the cost of such social harms. The proposed setup captures many well-studied special cases and is more general than existing formulations of multi-agent reinforcement learning with mechanism design in two ways: (i) the underlying environment is a history-based general reinforcement learning environment like in AIXI; (ii) the reinforcement-learning agents participating in the environment can have different learning strategies and planning horizons. To demonstrate the practicality of the proposed setup, we survey some key classes of learning algorithms and present a few applications, including a discussion of the Paperclips problem and pollution control with a cap-and-trade system.

Privacy Preserving Reinforcement Learning for Population Processes

We consider the problem of privacy protection in Reinforcement Learning (RL) algorithms that operate over population processes, a practical but understudied setting that includes, for example, the control of epidemics in large populations of dynamically interacting individuals. In this setting, the RL algorithm interacts with the population over $T$ time steps by receiving population-level statistics as state and performing actions which can affect the entire population at each time step. An individual's data can be collected across multiple interactions and their privacy must be protected at all times. We clarify the Bayesian semantics of Differential Privacy (DP) in the presence of correlated data in population processes through a Pufferfish Privacy analysis. We then give a meta algorithm that can take any RL algorithm as input and make it differentially private. This is achieved by taking an approach that uses DP mechanisms to privatize the state and reward signal at each time step before the RL algorithm receives them as input. Our main theoretical result shows that the value-function approximation error when applying standard RL algorithms directly to the privatized states shrinks quickly as the population size and privacy budget increase. This highlights that reasonable privacy-utility trade-offs are possible for differentially private RL algorithms in population processes. Our theoretical findings are validated by experiments performed on a simulated epidemic control problem over large population sizes.

Dynamic Knowledge Injection for AIXI Agents

Prior approximations of AIXI, a Bayesian optimality notion for general reinforcement learning, can only approximate AIXI's Bayesian environment model using an a-priori defined set of models. This is a fundamental source of epistemic uncertainty for the agent in settings where the existence of systematic bias in the predefined model class cannot be resolved by simply collecting more data from the environment. We address this issue in the context of Human-AI teaming by considering a setup where additional knowledge for the agent in the form of new candidate models arrives from a human operator in an online fashion. We introduce a new agent called DynamicHedgeAIXI that maintains an exact Bayesian mixture over dynamically changing sets of models via a time-adaptive prior constructed from a variant of the Hedge algorithm. The DynamicHedgeAIXI agent is the richest direct approximation of AIXI known to date and comes with good performance guarantees. Experimental results on epidemic control on contact networks validates the agent's practical utility.

A Direct Approximation of AIXI Using Logical State Abstractions

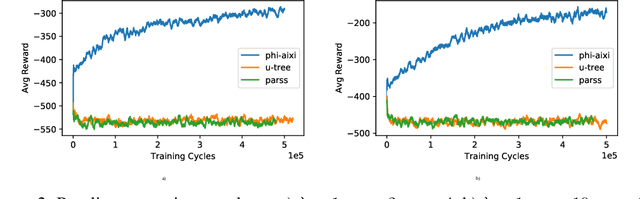
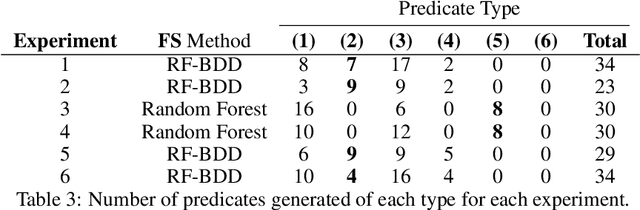
We propose a practical integration of logical state abstraction with AIXI, a Bayesian optimality notion for reinforcement learning agents, to significantly expand the model class that AIXI agents can be approximated over to complex history-dependent and structured environments. The state representation and reasoning framework is based on higher-order logic, which can be used to define and enumerate complex features on non-Markovian and structured environments. We address the problem of selecting the right subset of features to form state abstractions by adapting the $\Phi$-MDP optimisation criterion from state abstraction theory. Exact Bayesian model learning is then achieved using a suitable generalisation of Context Tree Weighting over abstract state sequences. The resultant architecture can be integrated with different planning algorithms. Experimental results on controlling epidemics on large-scale contact networks validates the agent's performance.

Factored Conditional Filtering: Tracking States and Estimating Parameters in High-Dimensional Spaces

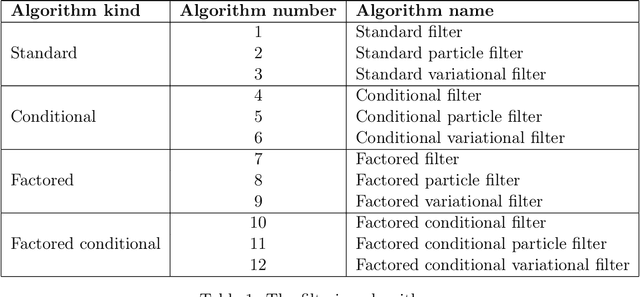
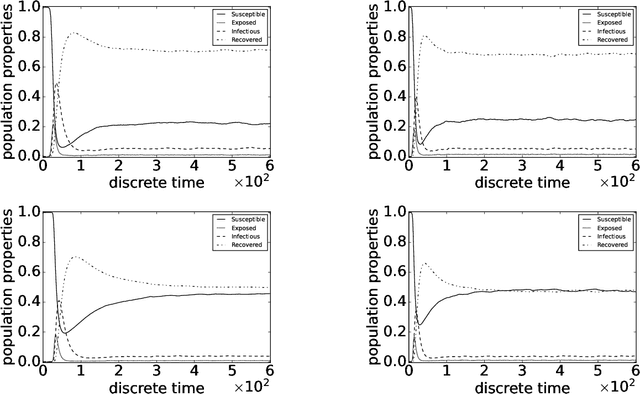
This paper introduces the factored conditional filter, a new filtering algorithm for simultaneously tracking states and estimating parameters in high-dimensional state spaces. The conditional nature of the algorithm is used to estimate parameters and the factored nature is used to decompose the state space into low-dimensional subspaces in such a way that filtering on these subspaces gives distributions whose product is a good approximation to the distribution on the entire state space. The conditions for successful application of the algorithm are that observations be available at the subspace level and that the transition model can be factored into local transition models that are approximately confined to the subspaces; these conditions are widely satisfied in computer science, engineering, and geophysical filtering applications. We give experimental results on tracking epidemics and estimating parameters in large contact networks that show the effectiveness of our approach.

Conditions on Features for Temporal Difference-Like Methods to Converge

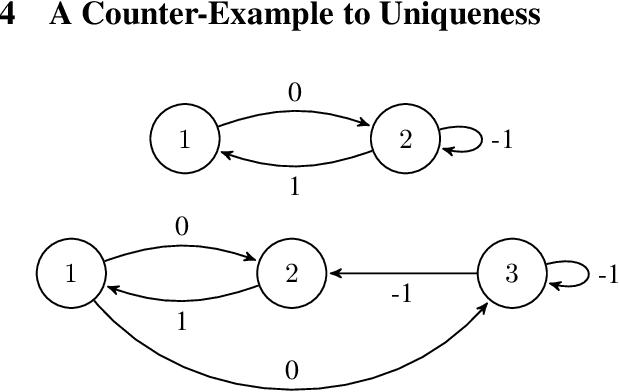
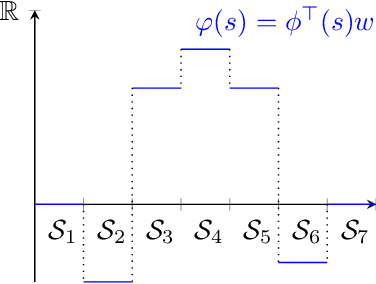
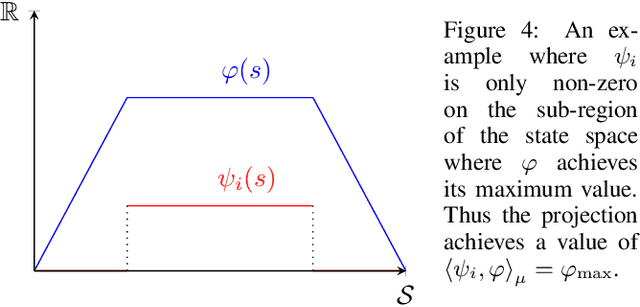
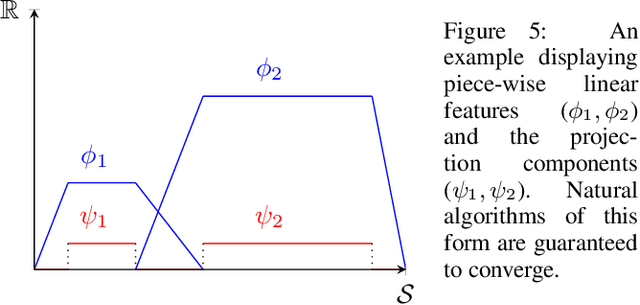
The convergence of many reinforcement learning (RL) algorithms with linear function approximation has been investigated extensively but most proofs assume that these methods converge to a unique solution. In this paper, we provide a complete characterization of non-uniqueness issues for a large class of reinforcement learning algorithms, simultaneously unifying many counter-examples to convergence in a theoretical framework. We achieve this by proving a new condition on features that can determine whether the convergence assumptions are valid or non-uniqueness holds. We consider a general class of RL methods, which we call natural algorithms, whose solutions are characterized as the fixed point of a projected Bellman equation (when it exists); notably, bootstrapped temporal difference-based methods such as $TD(\lambda)$ and $GTD(\lambda)$ are natural algorithms. Our main result proves that natural algorithms converge to the correct solution if and only if all the value functions in the approximation space satisfy a certain shape. This implies that natural algorithms are, in general, inherently prone to converge to the wrong solution for most feature choices even if the value function can be represented exactly. Given our results, we show that state aggregation based features are a safe choice for natural algorithms and we also provide a condition for finding convergent algorithms under other feature constructions.