Conditions on Features for Temporal Difference-Like Methods to Converge
Paper and Code
May 28, 2019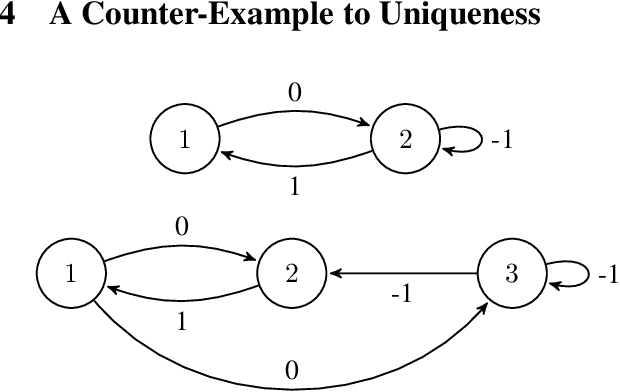
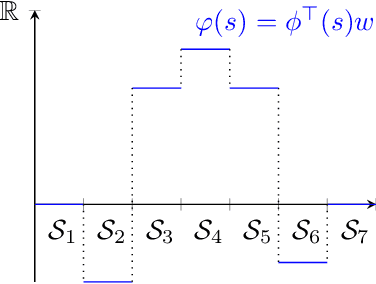
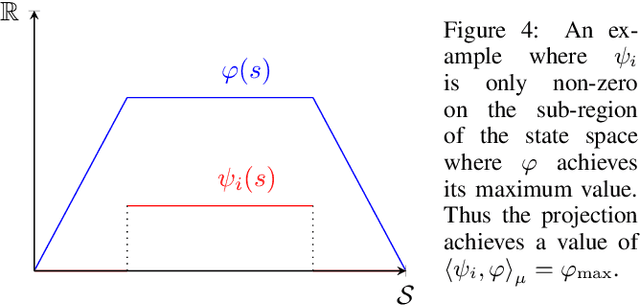
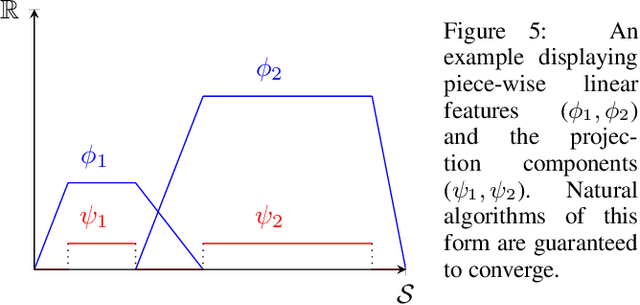
The convergence of many reinforcement learning (RL) algorithms with linear function approximation has been investigated extensively but most proofs assume that these methods converge to a unique solution. In this paper, we provide a complete characterization of non-uniqueness issues for a large class of reinforcement learning algorithms, simultaneously unifying many counter-examples to convergence in a theoretical framework. We achieve this by proving a new condition on features that can determine whether the convergence assumptions are valid or non-uniqueness holds. We consider a general class of RL methods, which we call natural algorithms, whose solutions are characterized as the fixed point of a projected Bellman equation (when it exists); notably, bootstrapped temporal difference-based methods such as $TD(\lambda)$ and $GTD(\lambda)$ are natural algorithms. Our main result proves that natural algorithms converge to the correct solution if and only if all the value functions in the approximation space satisfy a certain shape. This implies that natural algorithms are, in general, inherently prone to converge to the wrong solution for most feature choices even if the value function can be represented exactly. Given our results, we show that state aggregation based features are a safe choice for natural algorithms and we also provide a condition for finding convergent algorithms under other feature constructions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge