Abstractions of General Reinforcement Learning

The field of artificial intelligence (AI) is devoted to the creation of artificial decision-makers that can perform (at least) on par with the human counterparts on a domain of interest. Unlike the agents in traditional AI, the agents in artificial general intelligence (AGI) are required to replicate human intelligence in almost every domain of interest. Moreover, an AGI agent should be able to achieve this without (virtually any) further changes, retraining, or fine-tuning of the parameters. The real world is non-stationary, non-ergodic, and non-Markovian: we, humans, can neither revisit our past nor are the most recent observations sufficient statistics. Yet, we excel at a variety of complex tasks. Many of these tasks require longterm planning. We can associate this success to our natural faculty to abstract away task-irrelevant information from our overwhelming sensory experience. We make task-specific mental models of the world without much effort. Due to this ability to abstract, we can plan on a significantly compact representation of a task without much loss of performance. Not only this, we also abstract our actions to produce high-level plans: the level of action-abstraction can be anywhere between small muscle movements to a mental notion of "doing an action". It is natural to assume that any AGI agent competing with humans (at every plausible domain) should also have these abilities to abstract its experiences and actions. This thesis is an inquiry into the existence of such abstractions which aid efficient planing for a wide range of domains, and most importantly, these abstractions come with some optimality guarantees.

Reducing Planning Complexity of General Reinforcement Learning with Non-Markovian Abstractions

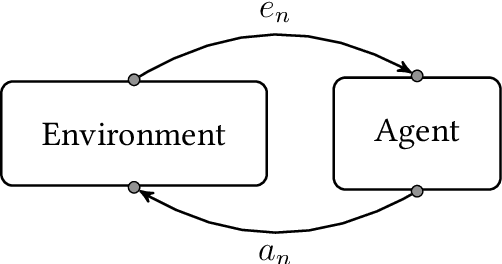
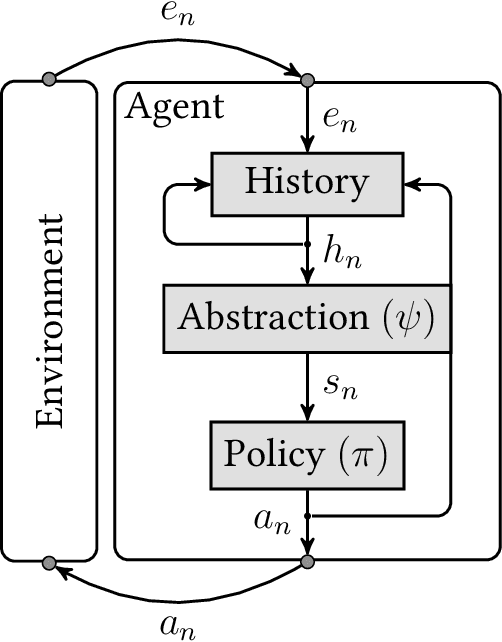
The field of General Reinforcement Learning (GRL) formulates the problem of sequential decision-making from ground up. The history of interaction constitutes a "ground" state of the system, which never repeats. On the one hand, this generality allows GRL to model almost every domain possible, e.g.\ Bandits, MDPs, POMDPs, PSRs, and history-based environments. On the other hand, in general, the near-optimal policies in GRL are functions of complete history, which hinders not only learning but also planning in GRL. The usual way around for the planning part is that the agent is given a Markovian abstraction of the underlying process. So, it can use any MDP planning algorithm to find a near-optimal policy. The Extreme State Aggregation (ESA) framework has extended this idea to non-Markovian abstractions without compromising on the possibility of planning through a (surrogate) MDP. A distinguishing feature of ESA is that it proves an upper bound of $O\left(\varepsilon^{-A} \cdot (1-\gamma)^{-2A}\right)$ on the number of states required for the surrogate MDP (where $A$ is the number of actions, $\gamma$ is the discount-factor, and $\varepsilon$ is the optimality-gap) which holds \emph{uniformly} for \emph{all} domains. While the possibility of a universal bound is quite remarkable, we show that this bound is very loose. We propose a novel non-MDP abstraction which allows for a much better upper bound of $O\left(\varepsilon^{-1} \cdot (1-\gamma)^{-2} \cdot A \cdot 2^{A}\right)$. Furthermore, we show that this bound can be improved further to $O\left(\varepsilon^{-1} \cdot (1-\gamma)^{-2} \cdot \log^3 A \right)$ by using an action-sequentialization method.

Conditions on Features for Temporal Difference-Like Methods to Converge

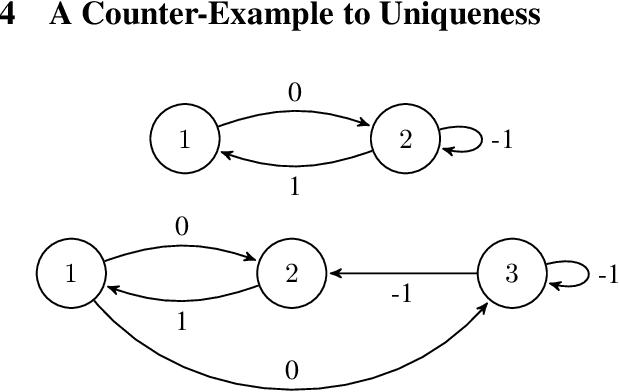
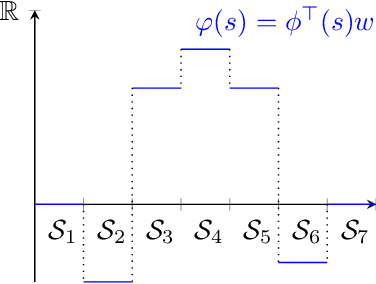
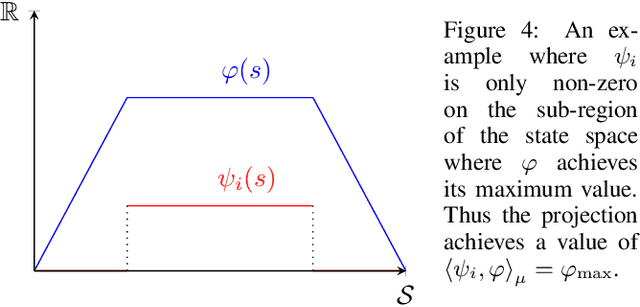
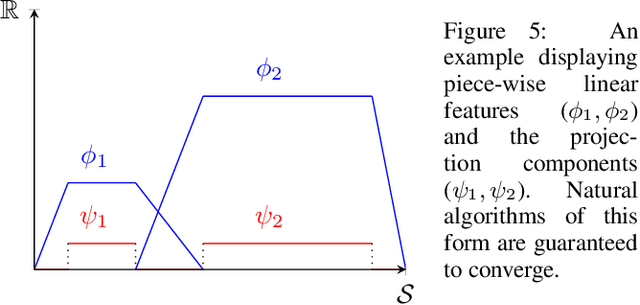
The convergence of many reinforcement learning (RL) algorithms with linear function approximation has been investigated extensively but most proofs assume that these methods converge to a unique solution. In this paper, we provide a complete characterization of non-uniqueness issues for a large class of reinforcement learning algorithms, simultaneously unifying many counter-examples to convergence in a theoretical framework. We achieve this by proving a new condition on features that can determine whether the convergence assumptions are valid or non-uniqueness holds. We consider a general class of RL methods, which we call natural algorithms, whose solutions are characterized as the fixed point of a projected Bellman equation (when it exists); notably, bootstrapped temporal difference-based methods such as $TD(\lambda)$ and $GTD(\lambda)$ are natural algorithms. Our main result proves that natural algorithms converge to the correct solution if and only if all the value functions in the approximation space satisfy a certain shape. This implies that natural algorithms are, in general, inherently prone to converge to the wrong solution for most feature choices even if the value function can be represented exactly. Given our results, we show that state aggregation based features are a safe choice for natural algorithms and we also provide a condition for finding convergent algorithms under other feature constructions.