Kazuyuki Tanaka
Relaxation-assisted reverse annealing on nonnegative/binary matrix factorization
Jan 03, 2025
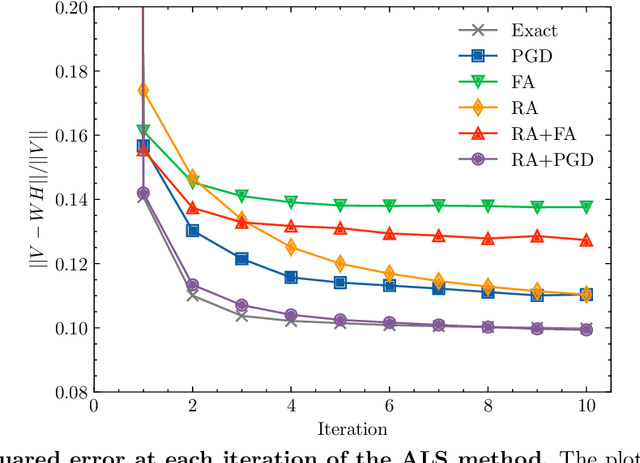
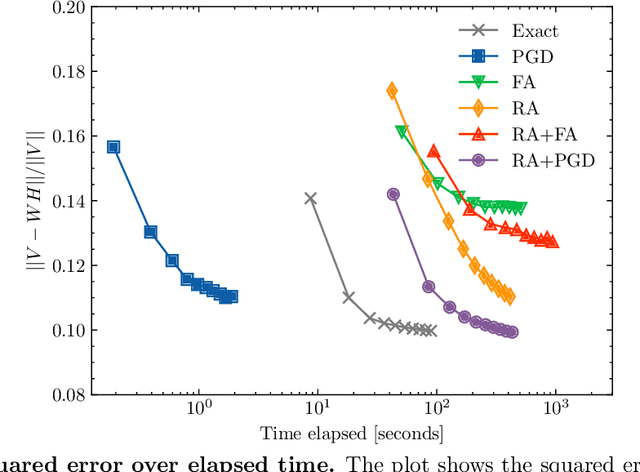
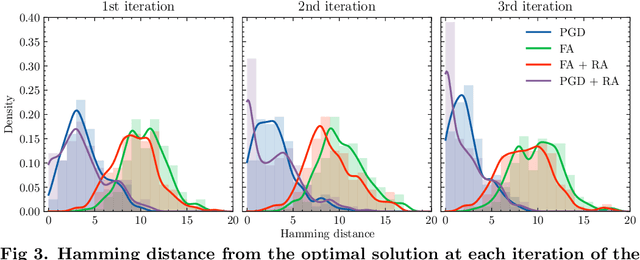
Abstract:Quantum annealing has garnered significant attention as meta-heuristics inspired by quantum physics for combinatorial optimization problems. Among its many applications, nonnegative/binary matrix factorization stands out for its complexity and relevance in unsupervised machine learning. The use of reverse annealing, a derivative procedure of quantum annealing to prioritize the search in a vicinity under a given initial state, helps improve its optimization performance in matrix factorization. This study proposes an improved strategy that integrates reverse annealing with a linear programming relaxation technique. Using relaxed solutions as the initial configuration for reverse annealing, we demonstrate improvements in optimization performance comparable to the exact optimization methods. Our experiments on facial image datasets show that our method provides better convergence than known reverse annealing methods. Furthermore, we investigate the effectiveness of relaxation-based initialization methods on randomized datasets, demonstrating a relationship between the relaxed solution and the optimal solution. This research underscores the potential of combining reverse annealing and classical optimization strategies to enhance optimization performance.
Travel time optimization on multi-AGV routing by reverse annealing
Apr 25, 2022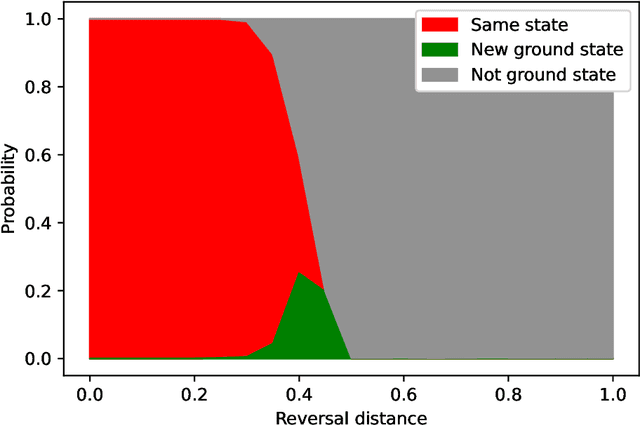

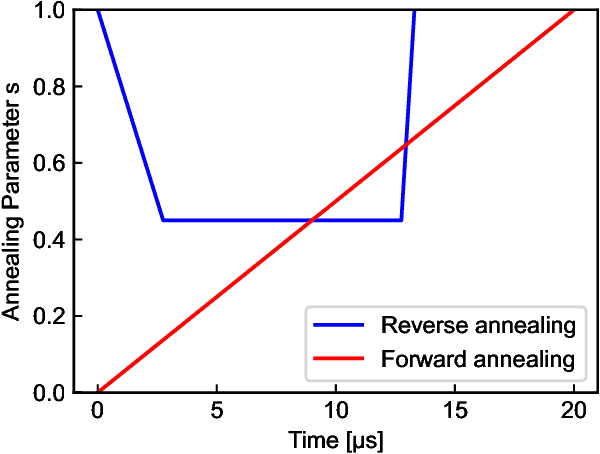
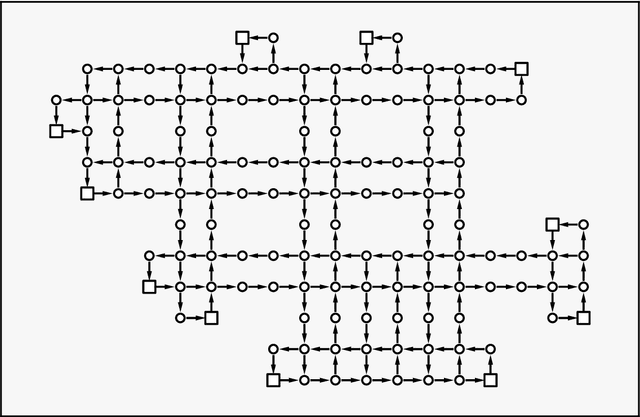
Abstract:Quantum annealing has been actively researched since D-Wave Systems produced the first commercial machine in 2011. Controlling a large fleet of automated guided vehicles is one of the real-world applications utilizing quantum annealing. In this study, we propose a formulation to control the traveling routes to minimize the travel time. We validate our formulation through simulation in a virtual plant and authenticate the effectiveness for faster distribution compared to a greedy algorithm that does not consider the overall detour distance. Furthermore, we utilize reverse annealing to maximize the advantage of the D-Wave's quantum annealer. Starting from relatively good solutions obtained by a fast greedy algorithm, reverse annealing searches for better solutions around them. Our reverse annealing method improves the performance compared to standard quantum annealing alone and performs up to 10 times faster than the strong classical solver, Gurobi. This study extends a use of optimization with general problem solvers in the application of multi-AGV systems and reveals the potential of reverse annealing as an optimizer.
Assessment of image generation by quantum annealer
Mar 15, 2021



Abstract:Quantum annealing was originally proposed as an approach for solving combinatorial optimisation problems using quantum effects. D-Wave Systems has released a production model of quantum annealing hardware. However, the inherent noise and various environmental factors in the hardware hamper the determination of optimal solutions. In addition, the freezing effect in regions with weak quantum fluctuations generates outputs approximately following a Gibbs--Boltzmann distribution at an extremely low temperature. Thus, a quantum annealer may also serve as a fast sampler for the Ising spin-glass problem, and several studies have investigated Boltzmann machine learning using a quantum annealer. Previous developments have focused on comparing the performance in the standard distance of the resulting distributions between conventional methods in classical computers and sampling by a quantum annealer. In this study, we focused on the performance of a quantum annealer as a generative model. To evaluate its performance, we prepared a discriminator given by a neural network trained on an a priori dataset. The evaluation results show a higher performance of quantum annealing compared with the classical approach for Boltzmann machine learning.
Momentum-Space Renormalization Group Transformation in Bayesian Image Modeling by Gaussian Graphical Model
Mar 20, 2018
Abstract:A new Bayesian modeling method is proposed by combining the maximization of the marginal likelihood with a momentum-space renormalization group transformation for Gaussian graphical models. Moreover, we present a scheme for computint the statistical averages of hyperparameters and mean square errors in our proposed method based on a momentumspace renormalization transformation.
Deep Neural Network Detects Quantum Phase Transition
Dec 01, 2017


Abstract:We detect the quantum phase transition of a quantum many-body system by mapping the observed results of the quantum state onto a neural network. In the present study, we utilized the simplest case of a quantum many-body system, namely a one-dimensional chain of Ising spins with the transverse Ising model. We prepared several spin configurations, which were obtained using repeated observations of the model for a particular strength of the transverse field, as input data for the neural network. Although the proposed method can be employed using experimental observations of quantum many-body systems, we tested our technique with spin configurations generated by a quantum Monte Carlo simulation without initial relaxation. The neural network successfully classified the strength of transverse field only from the spin configurations, leading to consistent estimations of the critical point of our model $\Gamma_c =J$.
* 4pages,3 figures
Susceptibility Propagation by Using Diagonal Consistency
Dec 01, 2017


Abstract:A susceptibility propagation that is constructed by combining a belief propagation and a linear response method is used for approximate computation for Markov random fields. Herein, we formulate a new, improved susceptibility propagation by using the concept of a diagonal matching method that is based on mean-field approaches to inverse Ising problems. The proposed susceptibility propagation is robust for various network structures, and it is reduced to the ordinary susceptibility propagation and to the adaptive Thouless-Anderson-Palmer equation in special cases.
Community Detection Algorithm Combining Stochastic Block Model and Attribute Data Clustering
Jul 21, 2016



Abstract:We propose a new algorithm to detect the community structure in a network that utilizes both the network structure and vertex attribute data. Suppose we have the network structure together with the vertex attribute data, that is, the information assigned to each vertex associated with the community to which it belongs. The problem addressed this paper is the detection of the community structure from the information of both the network structure and the vertex attribute data. Our approach is based on the Bayesian approach that models the posterior probability distribution of the community labels. The detection of the community structure in our method is achieved by using belief propagation and an EM algorithm. We numerically verified the performance of our method using computer-generated networks and real-world networks.
Statistical Analysis of Loopy Belief Propagation in Random Fields
Sep 13, 2015



Abstract:Loopy belief propagation (LBP), which is equivalent to the Bethe approximation in statistical mechanics, is a message-passing-type inference method that is widely used to analyze systems based on Markov random fields (MRFs). In this paper, we propose a message-passing-type method to analytically evaluate the quenched average of LBP in random fields by using the replica cluster variation method. The proposed analytical method is applicable to general pair-wise MRFs with random fields whose distributions differ from each other and can give the quenched averages of the Bethe free energies over random fields, which are consistent with numerical results. The order of its computational cost is equivalent to that of standard LBP. In the latter part of this paper, we describe the application of the proposed method to Bayesian image restoration, in which we observed that our theoretical results are in good agreement with the numerical results for natural images.
Bayesian Reconstruction of Missing Observations
Mar 26, 2015



Abstract:We focus on an interpolation method referred to Bayesian reconstruction in this paper. Whereas in standard interpolation methods missing data are interpolated deterministically, in Bayesian reconstruction, missing data are interpolated probabilistically using a Bayesian treatment. In this paper, we address the framework of Bayesian reconstruction and its application to the traffic data reconstruction problem in the field of traffic engineering. In the latter part of this paper, we describe the evaluation of the statistical performance of our Bayesian traffic reconstruction model using a statistical mechanical approach and clarify its statistical behavior.
Inverse Renormalization Group Transformation in Bayesian Image Segmentations
Jan 05, 2015

Abstract:A new Bayesian image segmentation algorithm is proposed by combining a loopy belief propagation with an inverse real space renormalization group transformation to reduce the computational time. In results of our experiment, we observe that the proposed method can reduce the computational time to less than one-tenth of that taken by conventional Bayesian approaches.
* 6 pages, 2 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge