Relaxation-assisted reverse annealing on nonnegative/binary matrix factorization
Paper and Code
Jan 03, 2025
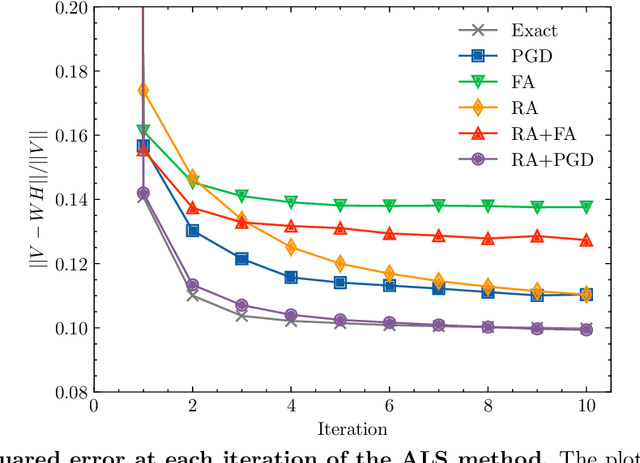
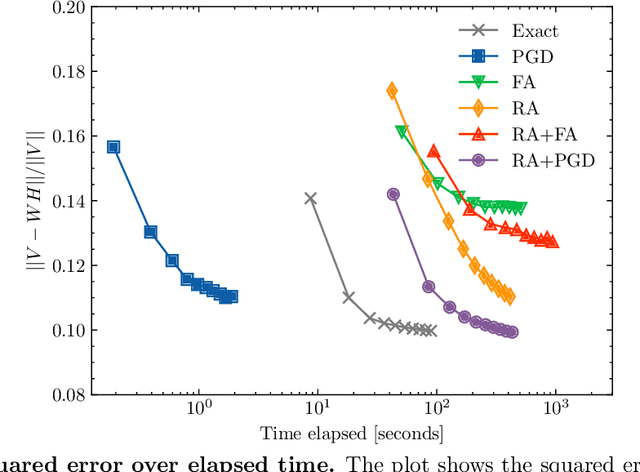
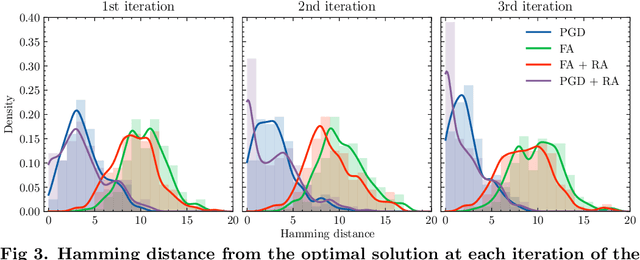
Quantum annealing has garnered significant attention as meta-heuristics inspired by quantum physics for combinatorial optimization problems. Among its many applications, nonnegative/binary matrix factorization stands out for its complexity and relevance in unsupervised machine learning. The use of reverse annealing, a derivative procedure of quantum annealing to prioritize the search in a vicinity under a given initial state, helps improve its optimization performance in matrix factorization. This study proposes an improved strategy that integrates reverse annealing with a linear programming relaxation technique. Using relaxed solutions as the initial configuration for reverse annealing, we demonstrate improvements in optimization performance comparable to the exact optimization methods. Our experiments on facial image datasets show that our method provides better convergence than known reverse annealing methods. Furthermore, we investigate the effectiveness of relaxation-based initialization methods on randomized datasets, demonstrating a relationship between the relaxed solution and the optimal solution. This research underscores the potential of combining reverse annealing and classical optimization strategies to enhance optimization performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge