Momentum-Space Renormalization Group Transformation in Bayesian Image Modeling by Gaussian Graphical Model

A new Bayesian modeling method is proposed by combining the maximization of the marginal likelihood with a momentum-space renormalization group transformation for Gaussian graphical models. Moreover, we present a scheme for computint the statistical averages of hyperparameters and mean square errors in our proposed method based on a momentumspace renormalization transformation.

Linear-Time Algorithm in Bayesian Image Denoising based on Gaussian Markov Random Field

In this paper, we consider Bayesian image denoising based on a Gaussian Markov random field (GMRF) model, for which we propose an new algorithm. Our method can solve Bayesian image denoising problems, including hyperparameter estimation, in $O(n)$-time, where $n$ is the number of pixels in a given image. From the perspective of the order of the computational time, this is a state-of-the-art algorithm for the present problem setting. Moreover, the results of our numerical experiments we show our method is in fact effective in practice.

Solving Non-parametric Inverse Problem in Continuous Markov Random Field using Loopy Belief Propagation

In this paper, we address the inverse problem, or the statistical machine learning problem, in Markov random fields with a non-parametric pair-wise energy function with continuous variables. The inverse problem is formulated by maximum likelihood estimation. The exact treatment of maximum likelihood estimation is intractable because of two problems: (1) it includes the evaluation of the partition function and (2) it is formulated in the form of functional optimization. We avoid Problem (1) by using Bethe approximation. Bethe approximation is an approximation technique equivalent to the loopy belief propagation. Problem (2) can be solved by using orthonormal function expansion. Orthonormal function expansion can reduce a functional optimization problem to a function optimization problem. Our method can provide an analytic form of the solution of the inverse problem within the framework of Bethe approximation.

Community Detection Algorithm Combining Stochastic Block Model and Attribute Data Clustering

We propose a new algorithm to detect the community structure in a network that utilizes both the network structure and vertex attribute data. Suppose we have the network structure together with the vertex attribute data, that is, the information assigned to each vertex associated with the community to which it belongs. The problem addressed this paper is the detection of the community structure from the information of both the network structure and the vertex attribute data. Our approach is based on the Bayesian approach that models the posterior probability distribution of the community labels. The detection of the community structure in our method is achieved by using belief propagation and an EM algorithm. We numerically verified the performance of our method using computer-generated networks and real-world networks.

Statistical Analysis of Loopy Belief Propagation in Random Fields

Loopy belief propagation (LBP), which is equivalent to the Bethe approximation in statistical mechanics, is a message-passing-type inference method that is widely used to analyze systems based on Markov random fields (MRFs). In this paper, we propose a message-passing-type method to analytically evaluate the quenched average of LBP in random fields by using the replica cluster variation method. The proposed analytical method is applicable to general pair-wise MRFs with random fields whose distributions differ from each other and can give the quenched averages of the Bethe free energies over random fields, which are consistent with numerical results. The order of its computational cost is equivalent to that of standard LBP. In the latter part of this paper, we describe the application of the proposed method to Bayesian image restoration, in which we observed that our theoretical results are in good agreement with the numerical results for natural images.

Bayesian Reconstruction of Missing Observations

We focus on an interpolation method referred to Bayesian reconstruction in this paper. Whereas in standard interpolation methods missing data are interpolated deterministically, in Bayesian reconstruction, missing data are interpolated probabilistically using a Bayesian treatment. In this paper, we address the framework of Bayesian reconstruction and its application to the traffic data reconstruction problem in the field of traffic engineering. In the latter part of this paper, we describe the evaluation of the statistical performance of our Bayesian traffic reconstruction model using a statistical mechanical approach and clarify its statistical behavior.

Inverse Renormalization Group Transformation in Bayesian Image Segmentations

A new Bayesian image segmentation algorithm is proposed by combining a loopy belief propagation with an inverse real space renormalization group transformation to reduce the computational time. In results of our experiment, we observe that the proposed method can reduce the computational time to less than one-tenth of that taken by conventional Bayesian approaches.

Bayesian image segmentations by Potts prior and loopy belief propagation

This paper presents a Bayesian image segmentation model based on Potts prior and loopy belief propagation. The proposed Bayesian model involves several terms, including the pairwise interactions of Potts models, and the average vectors and covariant matrices of Gauss distributions in color image modeling. These terms are often referred to as hyperparameters in statistical machine learning theory. In order to determine these hyperparameters, we propose a new scheme for hyperparameter estimation based on conditional maximization of entropy in the Potts prior. The algorithm is given based on loopy belief propagation. In addition, we compare our conditional maximum entropy framework with the conventional maximum likelihood framework, and also clarify how the first order phase transitions in LBP's for Potts models influence our hyperparameter estimation procedures.

Composite Likelihood Estimation for Restricted Boltzmann machines

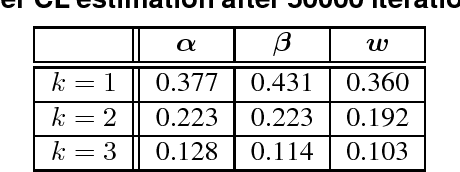
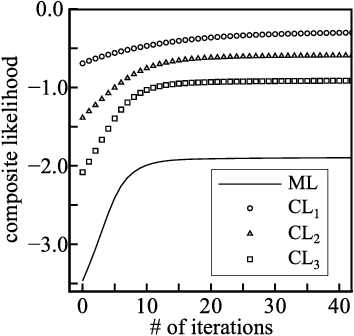
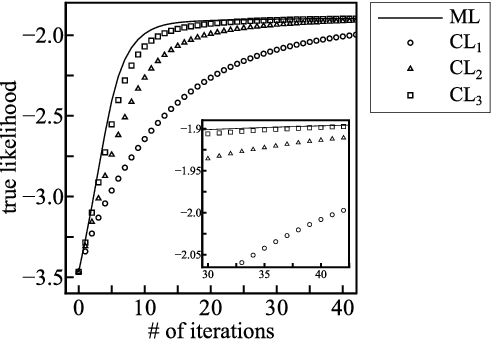
Learning the parameters of graphical models using the maximum likelihood estimation is generally hard which requires an approximation. Maximum composite likelihood estimations are statistical approximations of the maximum likelihood estimation which are higher-order generalizations of the maximum pseudo-likelihood estimation. In this paper, we propose a composite likelihood method and investigate its property. Furthermore, we apply our composite likelihood method to restricted Boltzmann machines.

Traffic data reconstruction based on Markov random field modeling

We consider the traffic data reconstruction problem. Suppose we have the traffic data of an entire city that are incomplete because some road data are unobserved. The problem is to reconstruct the unobserved parts of the data. In this paper, we propose a new method to reconstruct incomplete traffic data collected from various traffic sensors. Our approach is based on Markov random field modeling of road traffic. The reconstruction is achieved by using mean-field method and a machine learning method. We numerically verify the performance of our method using realistic simulated traffic data for the real road network of Sendai, Japan.