Bayesian image segmentations by Potts prior and loopy belief propagation

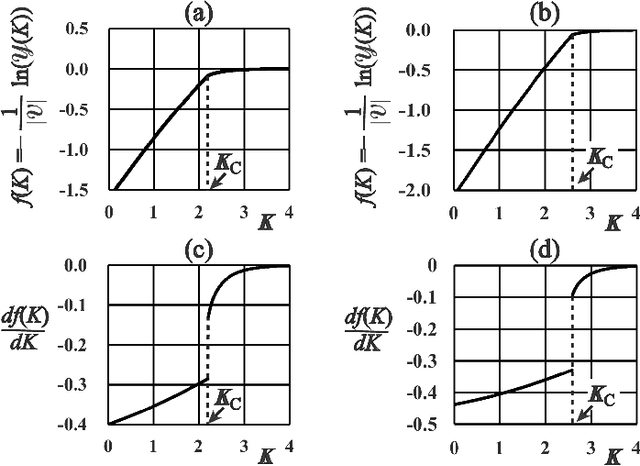
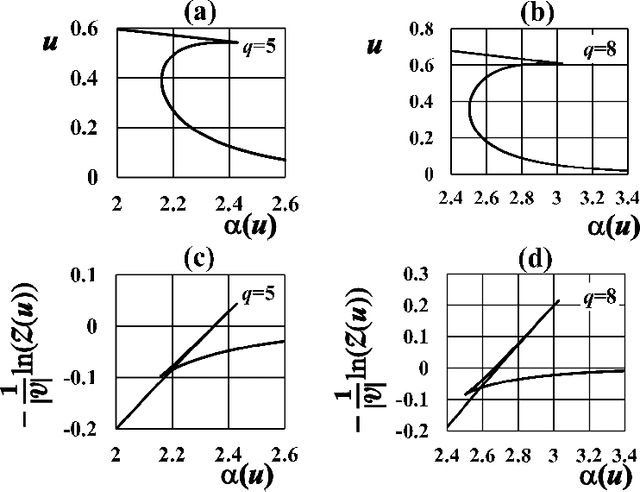
This paper presents a Bayesian image segmentation model based on Potts prior and loopy belief propagation. The proposed Bayesian model involves several terms, including the pairwise interactions of Potts models, and the average vectors and covariant matrices of Gauss distributions in color image modeling. These terms are often referred to as hyperparameters in statistical machine learning theory. In order to determine these hyperparameters, we propose a new scheme for hyperparameter estimation based on conditional maximization of entropy in the Potts prior. The algorithm is given based on loopy belief propagation. In addition, we compare our conditional maximum entropy framework with the conventional maximum likelihood framework, and also clarify how the first order phase transitions in LBP's for Potts models influence our hyperparameter estimation procedures.

Composite Likelihood Estimation for Restricted Boltzmann machines

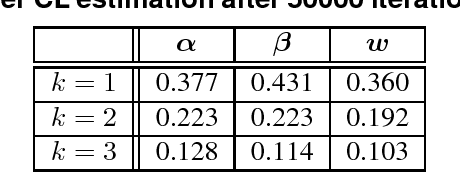
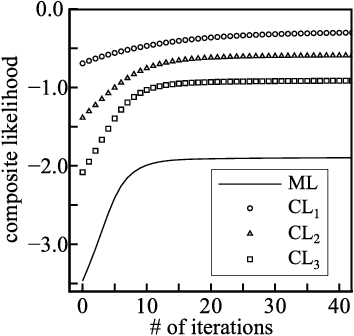
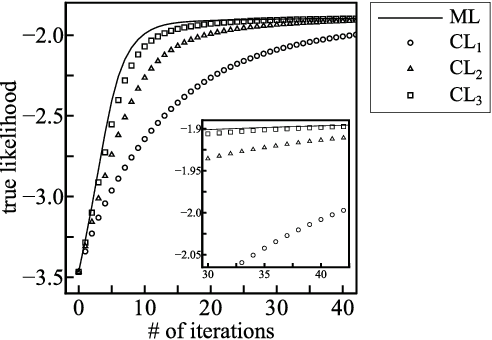
Learning the parameters of graphical models using the maximum likelihood estimation is generally hard which requires an approximation. Maximum composite likelihood estimations are statistical approximations of the maximum likelihood estimation which are higher-order generalizations of the maximum pseudo-likelihood estimation. In this paper, we propose a composite likelihood method and investigate its property. Furthermore, we apply our composite likelihood method to restricted Boltzmann machines.