GRADSTOP: Early Stopping of Gradient Descent via Posterior Sampling

Machine learning models are often learned by minimising a loss function on the training data using a gradient descent algorithm. These models often suffer from overfitting, leading to a decline in predictive performance on unseen data. A standard solution is early stopping using a hold-out validation set, which halts the minimisation when the validation loss stops decreasing. However, this hold-out set reduces the data available for training. This paper presents GRADSTOP, a novel stochastic early stopping method that only uses information in the gradients, which are produced by the gradient descent algorithm ``for free.'' Our main contributions are that we estimate the Bayesian posterior by the gradient information, define the early stopping problem as drawing sample from this posterior, and use the approximated posterior to obtain a stopping criterion. Our empirical evaluation shows that GRADSTOP achieves a small loss on test data and compares favourably to a validation-set-based stopping criterion. By leveraging the entire dataset for training, our method is particularly advantageous in data-limited settings, such as transfer learning. It can be incorporated as an optional feature in gradient descent libraries with only a small computational overhead. The source code is available at https://github.com/edahelsinki/gradstop.

Diffusion models as probabilistic neural operators for recovering unobserved states of dynamical systems

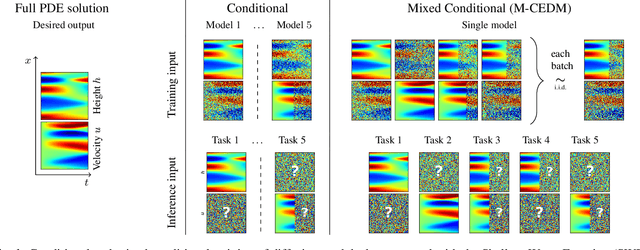
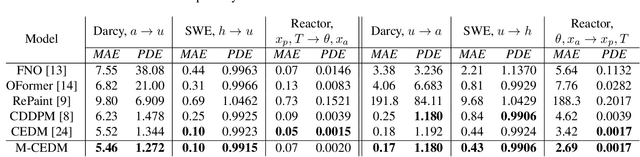
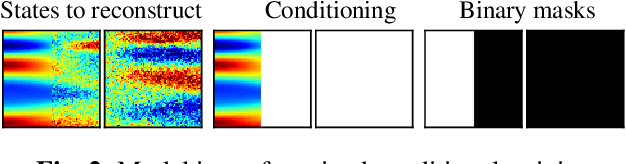
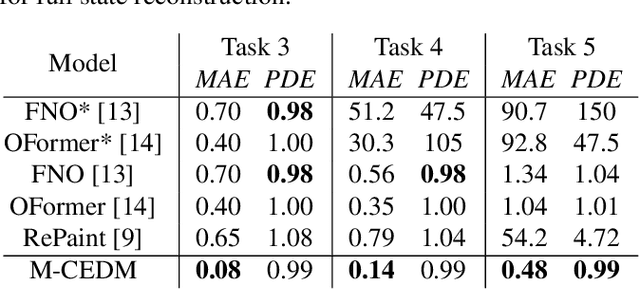
This paper explores the efficacy of diffusion-based generative models as neural operators for partial differential equations (PDEs). Neural operators are neural networks that learn a mapping from the parameter space to the solution space of PDEs from data, and they can also solve the inverse problem of estimating the parameter from the solution. Diffusion models excel in many domains, but their potential as neural operators has not been thoroughly explored. In this work, we show that diffusion-based generative models exhibit many properties favourable for neural operators, and they can effectively generate the solution of a PDE conditionally on the parameter or recover the unobserved parts of the system. We propose to train a single model adaptable to multiple tasks, by alternating between the tasks during training. In our experiments with multiple realistic dynamical systems, diffusion models outperform other neural operators. Furthermore, we demonstrate how the probabilistic diffusion model can elegantly deal with systems which are only partially identifiable, by producing samples corresponding to the different possible solutions.

In-Context Symbolic Regression: Leveraging Language Models for Function Discovery

Symbolic Regression (SR) is a task which aims to extract the mathematical expression underlying a set of empirical observations. Transformer-based methods trained on SR datasets detain the current state-of-the-art in this task, while the application of Large Language Models (LLMs) to SR remains unexplored. This work investigates the integration of pre-trained LLMs into the SR pipeline, utilizing an approach that iteratively refines a functional form based on the prediction error it achieves on the observation set, until it reaches convergence. Our method leverages LLMs to propose an initial set of possible functions based on the observations, exploiting their strong pre-training prior. These functions are then iteratively refined by the model itself and by an external optimizer for their coefficients. The process is repeated until the results are satisfactory. We then analyze Vision-Language Models in this context, exploring the inclusion of plots as visual inputs to aid the optimization process. Our findings reveal that LLMs are able to successfully recover good symbolic equations that fit the given data, outperforming SR baselines based on Genetic Programming, with the addition of images in the input showing promising results for the most complex benchmarks.

Improved Training of Physics-Informed Neural Networks with Model Ensembles

Learning the solution of partial differential equations (PDEs) with a neural network (known in the literature as a physics-informed neural network, PINN) is an attractive alternative to traditional solvers due to its elegancy, greater flexibility and the ease of incorporating observed data. However, training PINNs is notoriously difficult in practice. One problem is the existence of multiple simple (but wrong) solutions which are attractive for PINNs when the solution interval is too large. In this paper, we propose to expand the solution interval gradually to make the PINN converge to the correct solution. To find a good schedule for the solution interval expansion, we train an ensemble of PINNs. The idea is that all ensemble members converge to the same solution in the vicinity of observed data (e.g., initial conditions) while they may be pulled towards different wrong solutions farther away from the observations. Therefore, we use the ensemble agreement as the criterion for including new points for computing the loss derived from PDEs. We show experimentally that the proposed method can improve the accuracy of the found solution.

Learning Trajectories of Hamiltonian Systems with Neural Networks

Modeling of conservative systems with neural networks is an area of active research. A popular approach is to use Hamiltonian neural networks (HNNs) which rely on the assumptions that a conservative system is described with Hamilton's equations of motion. Many recent works focus on improving the integration schemes used when training HNNs. In this work, we propose to enhance HNNs with an estimation of a continuous-time trajectory of the modeled system using an additional neural network, called a deep hidden physics model in the literature. We demonstrate that the proposed integration scheme works well for HNNs, especially with low sampling rates, noisy and irregular observations.

A Grid-Structured Model of Tubular Reactors

We propose a grid-like computational model of tubular reactors. The architecture is inspired by the computations performed by solvers of partial differential equations which describe the dynamics of the chemical process inside a tubular reactor. The proposed model may be entirely based on the known form of the partial differential equations or it may contain generic machine learning components such as multi-layer perceptrons. We show that the proposed model can be trained using limited amounts of data to describe the state of a fixed-bed catalytic reactor. The trained model can reconstruct unmeasured states such as the catalyst activity using the measurements of inlet concentrations and temperatures along the reactor.