Diffusion models as probabilistic neural operators for recovering unobserved states of dynamical systems

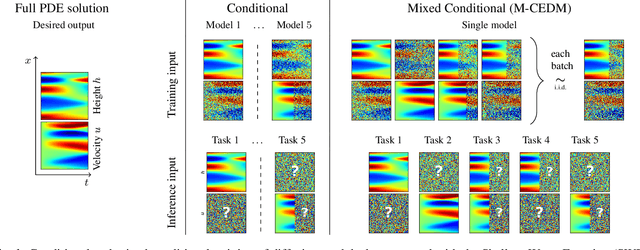
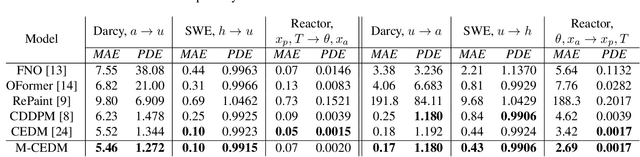
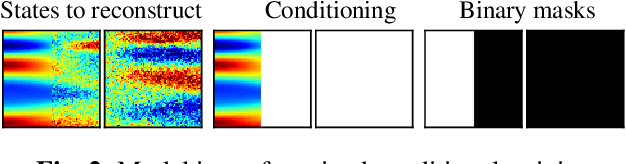
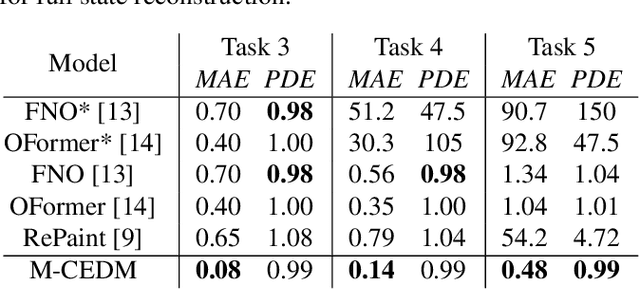
This paper explores the efficacy of diffusion-based generative models as neural operators for partial differential equations (PDEs). Neural operators are neural networks that learn a mapping from the parameter space to the solution space of PDEs from data, and they can also solve the inverse problem of estimating the parameter from the solution. Diffusion models excel in many domains, but their potential as neural operators has not been thoroughly explored. In this work, we show that diffusion-based generative models exhibit many properties favourable for neural operators, and they can effectively generate the solution of a PDE conditionally on the parameter or recover the unobserved parts of the system. We propose to train a single model adaptable to multiple tasks, by alternating between the tasks during training. In our experiments with multiple realistic dynamical systems, diffusion models outperform other neural operators. Furthermore, we demonstrate how the probabilistic diffusion model can elegantly deal with systems which are only partially identifiable, by producing samples corresponding to the different possible solutions.

Mixture of Coupled HMMs for Robust Modeling of Multivariate Healthcare Time Series

Analysis of multivariate healthcare time series data is inherently challenging: irregular sampling, noisy and missing values, and heterogeneous patient groups with different dynamics violating exchangeability. In addition, interpretability and quantification of uncertainty are critically important. Here, we propose a novel class of models, a mixture of coupled hidden Markov models (M-CHMM), and demonstrate how it elegantly overcomes these challenges. To make the model learning feasible, we derive two algorithms to sample the sequences of the latent variables in the CHMM: samplers based on (i) particle filtering and (ii) factorized approximation. Compared to existing inference methods, our algorithms are computationally tractable, improve mixing, and allow for likelihood estimation, which is necessary to learn the mixture model. Experiments on challenging real-world epidemiological and semi-synthetic data demonstrate the advantages of the M-CHMM: improved data fit, capacity to efficiently handle missing and noisy measurements, improved prediction accuracy, and ability to identify interpretable subsets in the data.