Diffusion models as probabilistic neural operators for recovering unobserved states of dynamical systems
Paper and Code
May 11, 2024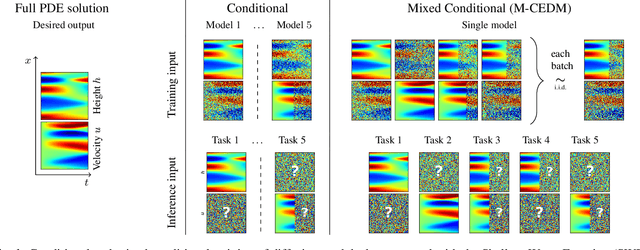
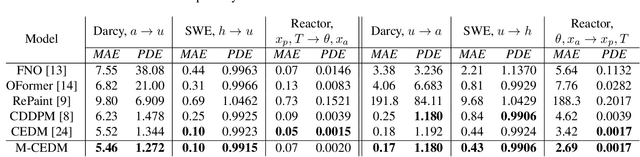
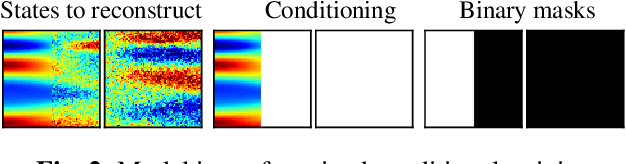
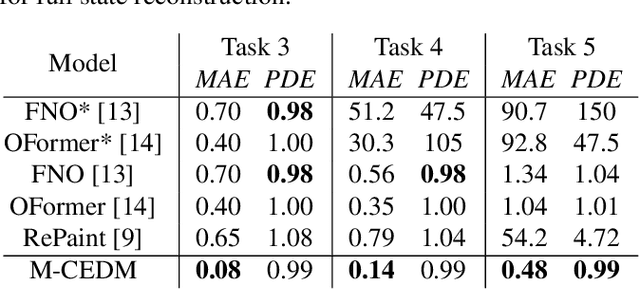
This paper explores the efficacy of diffusion-based generative models as neural operators for partial differential equations (PDEs). Neural operators are neural networks that learn a mapping from the parameter space to the solution space of PDEs from data, and they can also solve the inverse problem of estimating the parameter from the solution. Diffusion models excel in many domains, but their potential as neural operators has not been thoroughly explored. In this work, we show that diffusion-based generative models exhibit many properties favourable for neural operators, and they can effectively generate the solution of a PDE conditionally on the parameter or recover the unobserved parts of the system. We propose to train a single model adaptable to multiple tasks, by alternating between the tasks during training. In our experiments with multiple realistic dynamical systems, diffusion models outperform other neural operators. Furthermore, we demonstrate how the probabilistic diffusion model can elegantly deal with systems which are only partially identifiable, by producing samples corresponding to the different possible solutions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge