Cosmos 3: Omnimodal World Models for Physical AI

We introduce Cosmos 3, a family of omnimodal world models designed to jointly process and generate language, image, video, audio, and action sequences within a unified mixture-of-transformers architecture. By supporting highly flexible input-output configurations, Cosmos 3 seamlessly unifies critical modalities for Physical AI -- effectively subsuming vision-language models, video generators, world simulators, and world-action models into a single framework. Our evaluation demonstrates that Cosmos 3 establishes a new state-of-the-art across a diverse suite of understanding and generation tasks, demonstrating omnimodal world models as scalable, general-purpose backbones for embodied agents. Our post-trained Cosmos 3 models were ranked as the best open-source Text-to-Image and Image-to-Video models by Artificial Analysis, and the best policy model by RoboArena at the time the technical report was written. To accelerate open research and deployment in Physical AI, we make our code, model checkpoints, curated synthetic datasets, and evaluation benchmark available under the Linux Foundation's OpenMDW-1.1 https://openmdw.ai/license/1-1/ License at https://github.com/nvidia/cosmos}{github.com/nvidia/cosmos and https://huggingface.co/collections/nvidia/cosmos3 . The project website is available at https://research.nvidia.com/labs/cosmos-lab/cosmos3 .

Generalizing Gaussian Smoothing for Random Search

Gaussian smoothing (GS) is a derivative-free optimization (DFO) algorithm that estimates the gradient of an objective using perturbations of the current parameters sampled from a standard normal distribution. We generalize it to sampling perturbations from a larger family of distributions. Based on an analysis of DFO for non-convex functions, we propose to choose a distribution for perturbations that minimizes the mean squared error (MSE) of the gradient estimate. We derive three such distributions with provably smaller MSE than Gaussian smoothing. We conduct evaluations of the three sampling distributions on linear regression, reinforcement learning, and DFO benchmarks in order to validate our claims. Our proposal improves on GS with the same computational complexity, and are usually competitive with and often outperform Guided ES and Orthogonal ES, two computationally more expensive algorithms that adapt the covariance matrix of normally distributed perturbations.

Modeling and Optimization Trade-off in Meta-learning

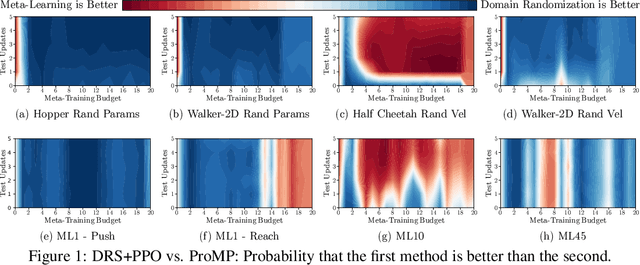
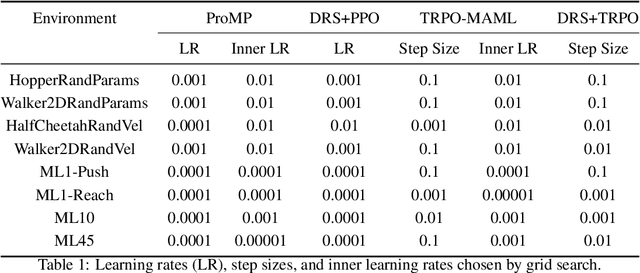
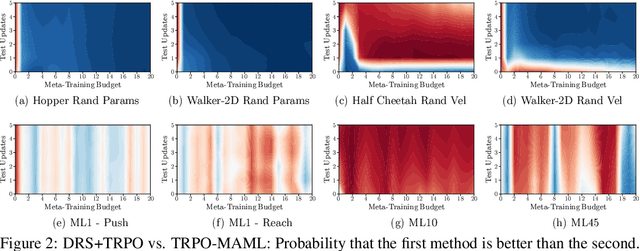
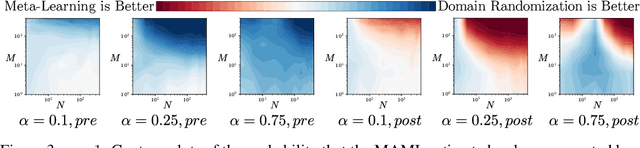
By searching for shared inductive biases across tasks, meta-learning promises to accelerate learning on novel tasks, but with the cost of solving a complex bilevel optimization problem. We introduce and rigorously define the trade-off between accurate modeling and optimization ease in meta-learning. At one end, classic meta-learning algorithms account for the structure of meta-learning but solve a complex optimization problem, while at the other end domain randomized search (otherwise known as joint training) ignores the structure of meta-learning and solves a single level optimization problem. Taking MAML as the representative meta-learning algorithm, we theoretically characterize the trade-off for general non-convex risk functions as well as linear regression, for which we are able to provide explicit bounds on the errors associated with modeling and optimization. We also empirically study this trade-off for meta-reinforcement learning benchmarks.

Assessing Generalization in Deep Reinforcement Learning

Deep reinforcement learning (RL) has achieved breakthrough results on many tasks, but has been shown to be sensitive to system changes at test time. As a result, building deep RL agents that generalize has become an active research area. Our aim is to catalyze and streamline community-wide progress on this problem by providing the first benchmark and a common experimental protocol for investigating generalization in RL. Our benchmark contains a diverse set of environments and our evaluation methodology covers both in-distribution and out-of-distribution generalization. To provide a set of baselines for future research, we conduct a systematic evaluation of deep RL algorithms, including those that specifically tackle the problem of generalization.

Confidence Intervals for Algorithmic Leveraging in Linear Regression

The age of big data has produced data sets that are computationally expensive to analyze and store. Algorithmic leveraging proposes that we sample observations from the original data set to generate a representative data set and then perform analysis on the representative data set. In this paper, we present efficient algorithms for constructing finite sample confidence intervals for each algorithmic leveraging estimated regression coefficient, with asymptotic coverage guarantees. In simulations, we confirm empirically that the confidence intervals have the desired coverage probabilities, while bootstrap confidence intervals may not.