Generalizing Gaussian Smoothing for Random Search
Paper and Code
Nov 27, 2022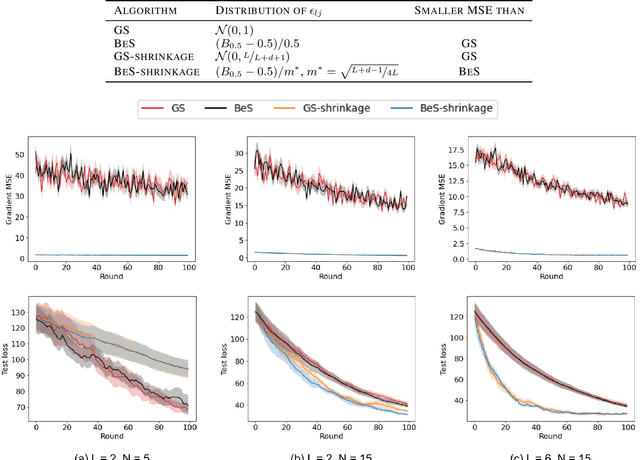
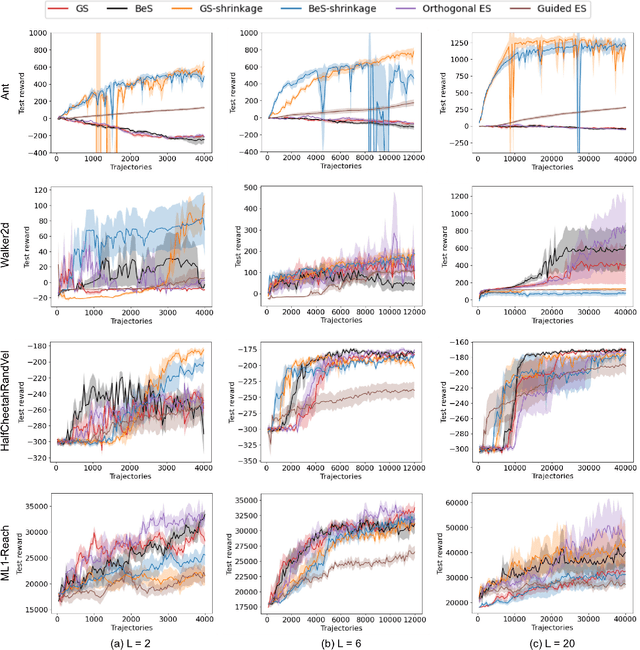
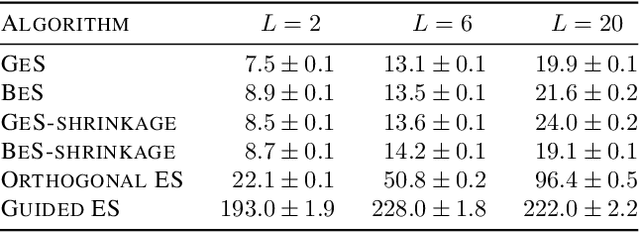
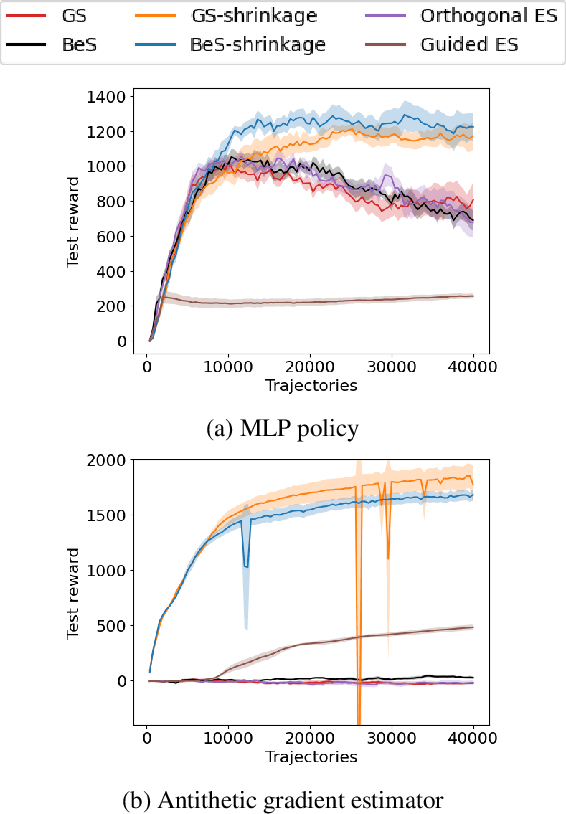
Gaussian smoothing (GS) is a derivative-free optimization (DFO) algorithm that estimates the gradient of an objective using perturbations of the current parameters sampled from a standard normal distribution. We generalize it to sampling perturbations from a larger family of distributions. Based on an analysis of DFO for non-convex functions, we propose to choose a distribution for perturbations that minimizes the mean squared error (MSE) of the gradient estimate. We derive three such distributions with provably smaller MSE than Gaussian smoothing. We conduct evaluations of the three sampling distributions on linear regression, reinforcement learning, and DFO benchmarks in order to validate our claims. Our proposal improves on GS with the same computational complexity, and are usually competitive with and often outperform Guided ES and Orthogonal ES, two computationally more expensive algorithms that adapt the covariance matrix of normally distributed perturbations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge